
Отчет Научного совета по катализу за 2004 г.
М.Г. Слинько "Эссе о нелинейности в катализе"
Терминология в гетерогенном катализе
под ред. Р.П.Бурвелла
Русский перевод
Ориганальная версия
За рубежом
Приглашения на конференции
Под эгидой Научного совета по катализу ОХНМ РАН (НСК) и при активном участии его членов были проведены следующие конференции и совещания:
В ежеквартальных выпусках "Каталитического бюллетеня" публикуется оперативная информация о важнейших результатах фундаментальных и прикладных исследований в области катализа в России и за рубежом, сведения об источниках дополнительного финансирования НИР (гранты, федеральные программы и т.д.), дается перечень предстоящих конференций, краткие отчеты о проведенных конференциях, школах и другие материалы.
Секретариат НСК продолжает сотрудничать с Академией наук, Министерствами, институтами разных ведомств и другими организациями России, дальнего и ближнего зарубежья по различным вопросам научной, научно-организационной, учебно-преподавательской и общественной деятельности в области катализа.
Примеры важнейших результатов
фундаментальных и прикладных исследований в области катализа,
полученных в 2004 году членами Академии наук или возглавляемыми ими коллективами
1. Селективное окисление насыщенных и ароматических углеводородов в спирты и фенолы
Разработан новый класс сопряженных каталитических реакций, позволяющих генерировать in situ из CCl4 (CBr4) и ROH (H2O) под действием катализатора Mo(CO)6 высокоактивные ROCl(Br) и HOCl(Br) для селективного окисления насыщенных и ароматических углеводородов в соответствующие спирты и фенолы.
Разработан перспективный для практического применения "one pot" метод жидкофазного окисления бензолов в фенолы с высокими выходами 78-90 %, основанный на реакции бензола или его алкил- или галогенпроизводных с HOBr или HOCl, генерируемыми in situ при взаимодействии CBr4 или CCl4 с H2O или спиртами под действием катализатора Mo(CO)6 при температуре 120 оС. Данный метод с успехом использован для окисления адамантанов в адамантанолы с выходами > 85 %, которые применяются в синтезе противовирусных препаратов (ремантадин, 3-гидрокси-ремантадин).
Член-корреспондент РАН У.М. Джемилев
Институт нефтехимии и катализа АН РБ и УНЦ РАН, Уфа
2. Каталитические наноматериалы на основе оксидов переходных металлов и молекулярных сит
Матричный синтез ультрадисперсных фаз простых, двойных и тройных оксидов переходных (Fe, Co) и непереходных (La, Sr) металлов в микро- и мезопористых молекулярных ситах осуществлен путем термоокислительного превращения моно- и полиядерных металлсодержащих соединений-предшественников непосредственно в порах носителей. Полученные материалы исследованы методами малоуглового РФА, ЭПР, ИКС, ЭСП, ДТА-ТГ, ТПВ, РФЭС, XAFS, локального зондового микроанализа, магнетометрии и адсорбции азота, а также изучена их активность в каталитическом окислении метанола. Показано, что матричный синтез не приводит к изменениям структуры и текстуры молекулярно-ситовых носителей, наночастицы сложных оксидов имеют однородный химический состав и равномерно распределены в объеме матрицы. В то же время по своим структурно-химическим и каталитическим свойствам они резко отличаются от объемных аналогов.
Академик В.В. Лунин
проф., д.х.н. Романовский Б.В.,
Московский государственный университет им.М.В.Ломоносова,
Химический факультет, Москва
3. Исследование механизмов гетерогенно-каталитических реакций с помощью спектроскопии ЯМР in situ
Методом спектроскопии ЯМР in situ исследованы механизмы метилирования ароматических соединений различных классов на цеолитных катализаторах. Предложены стадийный и синхронный механизмы алкилирования на кислотных цеолитах: первый из них включает взаимодействие метанола с бренстедовскими кислотными центрами и образование поверхностных метоксигрупп в качестве интермедиатов метилирования; второй, предположительно, реализуется через восьмичленное циклическое переходное состояние, включающее атомы цеолита, ароматического соединения и метанола или диметилового эфира, образующегося из метанола на первой стадии реакции. Показано, что направление алкилирования зависит от типа субстрата: толуол алкилируется в ароматическое кольцо, анилин - в функциональную группу, а фенол - как в ароматическое кольцо, так и в функциональную группу; продукты алкилирования в функциональную группу претерпевают далее изомеризацию с переносом метильной группы в ароматическое кольцо. Установлено, что дезактивация кислотных цеолитов в ходе алкилирования толуола и фенола связана с образованием конденсированных ароматических углеводородов, блокирующих поры цеолита, а в случае метилирования анилина - с образованием азотсодержащих гетероциклических соединений, отравляющих кислотные центры. Полученные экспериментальные данные и установленные на их основе механизмы каталитического действия цеолитов в процессах метилирования ароматических соединений могут быть использованы для научного прогнозирования каталитических свойств этих систем и создания научных основ приготовления эффективных катализаторов процессов алкилирования.
Академик В.В. Лунин
проф., д.х.н. И.И.Иванова,
Московский государственный университет им. М.В. Ломоносова,
Химический факультет, Москва
4. Катализ и фотокатализ фталоцианиновыми комплексами металлов в медицине
В процессе фотокаталитического окисления аскорбиновой кислоты в присутстви фталоцианиновых комплексов металлов (РсМ) установлена относительная роль маршрутов, включающих образование синглетного кислорода и маршрутов, инициированных переносом электрона с возбужденного фталоцианина на кислород. На этой основе предложено объяснение эффектов аскорбиновой кислоты в фотодинамической терапии рака.
В системе замещенный РсFe - легко окисляющийся субстрат - кислород зафиксировано эффективное образование пероксида водорода уже в индукционном периоде процесса образования окисленной формы субстрата.
Каталитическая система замещенный РсFe - пероксид водорода использована для экологически безопасного окисления трифениламина с получением N,N'-тетрафенилбензидина и более высокомолекулярных продуктов окислительного сочетания, перспективных в качестве электролюминесцентных материалов.
Академик Г.Н. Ворожцов,
Доктор химических наук,
профессор О.Л. Калия
ГНЦ "НИОПИК", Москва
5. Роль ионного состояния платины в формировании активных центров катализаторов риформинга
Разработан новый подход к получению алюмоплатиновой каталитической системы, позволяющий увеличить селективность формироâания "ионного" состояния платины через поверхностный синтез предшественника активного компонента - гидроксокомплексов платины как продукта лигандного обмена хлоридных лигандов комплексов Pt(IV) с поверхностными OH-группами носителя оксида алюминия.
Проведена оптимизация температуры и времени синтеза и оценена прочность закрепления адсорбированных комплексов платины на носителе в зависимости от степени их гидролиза на поверхности. Установлено, что предложенный подход закрепления гидролизованных форм платины приводит к образованию высокодисперсных систем с более прочной связью металл-носитель, что является перспективным в плане молекулярного дизайна определенных состояний активных форм нанесенной платины.
Исследование полученных систем в модельной реакции низкотемпературного гидрирования бензола показало уменьшение гидрирующей функции нанесенной платины по сравнению с традиционными алюмоплатиновыми катализаторами, что позволяет сделать предположения о формировании активных центров нового типа.
Член-корр. РАН В.А. Лихолобов,(ик) Институт проблем переработки углеводородов СО РАН, Омск
6. Новое поколение катализаторов и модернизация технологии риформинга для производства высокооктановых бензинов
Разработана технология производства новых катализаторов рèôорминга ПР- 51/04 и ПР- 71, включающая технологии: непрерывного осаждения гидроокиси алюминия; модифицирования оксида алюминия элементами IV группы периодической системы элементов; пластификации, формовки и прокалки в производстве носителя; вакуумного увлажнения и циркуляционной пропитки в производстве катализаторов серии ПР. Разработана техническая документация на производство новых катализаторов и проведены работы по модернизации технологических линий производства носителя и катализаторов риформинга на ЗАО "Промышленные катализаторы ТНК-ВР" в г. Рязань.
В 2004 г. в ЗАО "Промышленные катализаторы ТНК - ВР" выпущена первая промышленная партия катализатора ПР-51/ 04 в количестве 48,2 тонны. В мае 2004 г. катализатор загружен в реактор Р - 104 установки ЛЧ-35-11/1000 Лисичанского НПЗ ТНК - ВР.
Проведены промышленные испытания катализатора в режимах повышенной жесткости, а также определены данные материального баланса процесса по результатам двух фиксированных пробегов установки. В режиме выработки риформата с октановым числом ОИЧ=96 выход риформата составил 87,5-88 % масс., водорода 2,4-2,5% масс. В режиме выработки риформата с октановым числом ОИЧ=98-99 выход катализата составил 86,5 % масс., водорода 2,5-2,6% масс. Полученные результаты отражают высокий уровень эффективности работы нового катализатора.
Член-корреспондент РАН В.А. Лихолобов,
Д.х.н. А.С. Белый,
Институт проблем переработки углеводородов СО РАН, Омск
7. Восстановительная дегидратация алифатических спиртов- новая реакция в каталитическом синтезе алканов
После обработки диоксидом углерода каталитической композиции, состоящей из интерметаллического гидрида [TiFe0,95Zr0,03Mo0,02]Hx, и промышленного алюмоплатинового катализатора Pt/Al2O3, этанол, изобутиловый и изоамиловый спирты превращаются в алканы с, как минимум, удвоенным углеродным остовом исходного спирта. Выход алкановых фракций составляет 40, 60 и ~30 % масс., соответственно. Остальными продуктами являются кислородсодержащие и газообразные соединения. Состав алкановой фракции зависит от природы спирта:
2-метилпропанол-1 и 2-метилбутанол-1 селективно превращаются в продукты димеризации углеводородного остова спиртов - диметилгексан и диметилоктан, соответственно. В составе алкановых продуктов восстановительной дегидратации спиртов доминирующими продуктами являются изоалканы.
Академик И.И. Моисеев,
Институт общей и неорганической химии им. Н.С. Курнакова РАН,
Москва
8. Поиск путей управления селективностью процесса Фишера-Тропша в присутствии катализаторов на основе нанокластеров металлов VIII группы
Существенно расширен круг исходных реагентов - полиядерных комплексов палладия(II), никеля(II), кобальта(II), железа(II) и (III) с триметилацетатными лигандами, а также с "мягкими" N,S-донорными лигандами. Впервые синтезированы и структурно охарактеризованы методами элементного анализа, ИК и ЯМР-спектроскопии, рентгеноструктурного анализа и термогравиметрии 16 комплексов металлов VIII группы, содержащих от двух до девяти атомов металла, в том числе два гетерометаллических (Fe-Co, структура уточняется), и три полимерных комплекса.
Изучение химических свойств синтезированных полиядерных комплексов показало, что полиядерные комплексы палладия(II), кобальта(II) и никеля(II), в состав которых входят N,S-донорные лиганды, восстанавливаются под действием н-бутиллития и триэтилалюминия с образованием растворимых моно- и полиядерных комплексов этих металлов в близких к нулю степенях окисления, но не образуют нанокластеров. В отличие от этого, комплексы кобальта(II), никеля(II), железа(II) и железа(III) восстанавливаются под действием металлоорганических восстановителей с образованием растворимых в неполярных средах нанокластеров соответствующих металлов.
Новые кластеры кобальта и железа испытаны в качестве прекурсоров катализаторов синтеза углеводородов из CO и H2 (синтез Фишера-Тропша). Установлено, что введение нанокластеров кобальта в состав катализаторов Фишера-Тропша заметно влияет на селективность реакции и позволяет варьировать состав образующихся жидких углеводородов. Добавки гетерометаллических Co-Fe комплексов к стандартному промышленному катализатору в заметной степени стабилизируют активность катализатора во времени.
Академик И.И. Моисеев,
Институт общей и неорганической химии им. Н.С. Курнакова РАН,
Москва
9. Роль автокаталитических реакций на ранних стадиях биологической эволюции
В Институте катализа СО РАН проведено систематическое исследование механизма автокаталитической "формозной" реакции Бутлерова, которую рассматривают как одну из наиболее важных реакций химической предыстории жизни. В этой реакции из простейших молекул формальдегида синтезируются высшие сахара и, в частности, рибоза - важнейший компонент носителей биологической информации - молекул РНК и ДНК.
Обнаружено, что реакцию Бутлерова в проточном реакторе инициируют только С2- и С3-углеводы и сорбоза. Исследована возможность инициирования реакции Бутлерова УФ излучением. Идентифицированы основные продукты, образующиеся под его воздействием в нейтральном водном растворе формальдегида. Показано, что, обнаруженные среди продуктов в водном растворе, гликолевый и глицериновый альдегиды являются наиболее активными инициаторами реакции синтеза сахаров из формальдегида. Найдено, что образующихся количеств этих альдегидов вполне достаточно для инициирования реакции Бутлерова. Таким образом, на примере достаточно простой системы показана возможность осуществления естественного отбора в химических процессах на ранних стадиях эволюции.
Академик В.Н. Пармон,
К.ф-м.н В.Н. Снытников
Институт катализа им. Г.К. Борескова СО РАН, Новосибирск
10. Новые каталитические системы для безгалогенного карбонилирования диметилового эфира в метилацетат
В настоящее время более 60% уксусной кислоты производится путем карбонилирования метанола в жидкой фазе на гомогенном родиевом катализаторе с метилиодидом в качестве промотора.
Созданы новые каталитические системы на основе кислых цезиевых солей фосфорвольфрамовой ГПК с добавками родия для реакции безгалогенного карбонилирования диметилового эфира (ДМЭ) в метилацетат, которые позволяют значительно улучшить экологические и экономические показатели процесса за счет исключения метилиодида, проведения реакции в газовой фазе и замены метанола на более дешевое сырье - ДМЭ.
Академик В.Н. Пармон,
К.х.н. Г.Г. Волкова,
Институт катализа им. Г.К. Борескова СО РАН, Новосибирск
11. Промышленная технология доочистки хвостовых газов установок Клауса
В октябре 2004 г. введена в действие на Омском НПЗ промышленная установка на основе разработанной технологии селективного каталитического окисления H2S в серу для доочистки хвостовых газов установок Клауса. Технология основана на применении нового высокоселективного алюмо-железного катализатора ИКТ-27-42, разработанного в Институте катализа. Использование данной технологии позволяет существенно снизить выбросы диоксида серы в атмосферу на нефте- и газоперерабатывающих предприятиях, а также на предприятиях химической и металлургической промышленности. Технология характеризуется высокой степенью извлечения серы (до 99%) в сочетании с минимальными капитальными и эксплуатационными затратами по сравнению с ранее известными методами доочистки хвостовых газов.
Академик В.Н. Пармон,
К.т.н. А.Н. Загоруйко,
Институт катализа им. Г.К. Борескова СО РАН, Новосибирск
Председатель
Научного совета по катализу,
академик В.Н. Пармон
В гетерогенном катализе каталитическая активность поверхности обусловлена большим числом взаимодействующих атомов адсорбированных веществ и катализатора. Тонкий слой этих атомов представляет собой открытую, неравновесную, неидеальную, нелинейную, многопараметрическую, многомерную систему, обменивающуюся веществом и энергией, как с газовой, так и с твердой фазами. Поэтому теория и практика промышленного катализа опирается на теорию нелинейных динамических систем или, кратко, на нелинейную динамику.
При межмолекулярных взаимодействиях на поверхности катализатора присутствуют силы отталкивания и притяжения. Силы отталкивания на близких расстояниях экспоненциально спадают с расстоянием. Притяжение возникает на больших расстояниях, и оно пропорционально 1/Rn, где 4<n<6. Нелинейный закон Кулона является фундаментальным законом для описания сил, действующих на электрический заряд. Образующиеся связи являются ключом к нанотехнологии. Они объединяют атомы, ионы и молекулы в структуры, имеющие наноскопические размеры. Таким образом, нелинейные зависимости возникают на атомномолекулярном уровне, которые определяют нелинейный характер зависимости скорости реакций и на более высоких иерархических уровнях.
Процессы переноса вещества, тепла и импульса также влияют на характер нелинейных закономерностей протекающих каталитических процессов. Хотя практика катализа с самого рождения имела дело с нелинейными проблемами, нелинейная динамика каталитических процессов и реакторов развивалась лишь последние 25 лет.
Недостаточное внимание к нелинейным проблемам и исследованиям по нелинейной физике школы академика Л.И. Мандельштама на физическом факультете МГУ им. М.В. Ломоносова было характерно не только для каталитических работ. Так, в знаменитом многотомном курсе теоретической физики Ландау и Лифшица нет тома по нелинейной физике.
Ограниченность теоретических знаний о катализе, обусловленная линейной и квазилинейной структурой научного мышления, приводила к ошибкам в трактовке наблюдаемых результатов. Делались выводы о неизменности процессов вблизи и вдали от термодинамического равновесия, о постоянстве удельной активности катализатора и другие. В действительности явление катализа требует принципиально нелинейного подхода к описанию эволюционных процессов.
Обращение к нелинейным зависимостям наполнило наше знание о катализе совершенно новым содержанием. По существу речь идет о становлении нового раздела теории и практики катализа, который можно назвать нелинейной динамикой каталитических процессов. Развитие катализа показало, что каталитические процессы и реакторы невозможно описать на основе уравнений линейной теории.
1. Нелинейность
Нарушение принципа суперпозиции основная характеристика и свойство нелинейности. Нелинейность проявляется в различных областях. Она вездесуща, всепроникающая, многолика и неисчерпаемо многообразна. Она возникает на всех масштабах (микро - нано - мезо - макро мега) каталитических и химикотехнологических систем. Нелинейность проявляется в таких явлениях и эффектах, как множественность и неустойчивость стационарных состояний, самоорганизованная критичность, регулярные и хаотические автоколебания скорости реакции.
Характер процессов в нелинейной каталитической системе намного богаче, чем в линейной системе. В отличие от линейной системы, в которой либо все состояния устойчивы, либо все неустойчивы, в нелинейной системе могут существовать, как устойчивые, так и неустойчивые стационарные состояния. В связи с этим, при изучении устойчивости каталитических процессов в нелинейной системе вводятся понятия устойчивости в малом, устойчивости в области, устойчивости в целом.
Нелинейные явления и эффекты могут быть очень опасны. Сложность нелинейных, больших каталитических систем состоит в том, что в них часто незначительное изменение второстепенных величин приводит к катастрофическим последствиям. Примером может служить изменение концентрации дихлорэтана промотора в процессе получения окиси этилена из этиленкислородных смесей на серебряных катализаторах. Концентрация промотора дихлорэтана в газовой смеси равна ~3 ppm. При небольшом уменьшении концентрации промотора снижается избирательность окисления С2Н4. Резко возрастает тепловыделение, которое приводит к дальнейшему снижению избирательности, а, следовательно, и к дальнейшему возрастанию температуры. В результате могут возникнуть аварийные состояния реактора.
Изменение параметров каталитической системы может привести к качественному преобразованию фазового портрета системы, называемого бифуркацией. Под качественным изменением фазового портрета каталитической системы подразумевается ее структурная перестройка. Значение параметра, при котором происходит бифуркация, называется точкой бифуркации. Резкое изменение состояния системы под влиянием малых изменений параметров называется катастрофой. Анализ бифуркации при изменении параметров системы позволяет построить бифуркационную диаграмму. Эта диаграмма представляет собой набор точек, линий и поверхностей в пространстве параметров, которые соответствуют различным бифуркациям. Знание такой диаграммы позволяет избежать катастроф в практических условиях и дает цельное представление о каталитическом процессе.
Надо иметь в виду, что развитие каталитических систем происходит нелинейно и неоднозначно. В точках бифуркации малые воздействия могут дать большой эффект. В окрестности неустойчивого состояния эти воздействия являются случайными, не учтенными заранее. Теория катастроф описывает скачкообразные изменения каталитических процессов.
Одним из фундаментальных открытий нелинейной, необратимой термодинамики за последние годы является обнаружение конструктивной роли необратимости. С возрастанием времени вместо стремления к хаотическому термодинамическому равновесию могут происходить противоположные процессы, и в результате возникают упорядоченные пространственно - временные структуры. Образование структур жестко связано с анализом неустойчивого стационарного состояния. Мы переходим в область нелинейной неравновесной термодинамики, уравнения которой становятся другими. Поэтому кинетические уравнения, получаемые вблизи равновесия, не могут быть использованы вдали от термодинамического равновесия. В ситуации, далекой от равновесия, дифференциальные уравнения, моделирующие каталитический процесс, становятся нелинейными, а линейные уравнения обычно имеют более чем один тип решения. И, что особенно удивительно, каталитический процесс может быть понят более глубоко в свете представлений, учитывающих как устойчивость, так и неустойчивость состояний. Неустойчивость, случайность, непредсказуемость стали играть немаловажную роль в понимании каталитических процессов.
2. Автоколебания
Открытие в 19721973 гг. автоколебаний скорости одновременно Хуго и Вике в реакции окисления CO на платиновом катализаторе и, одновременно, В.Д. Беляевым и М.М. Слинько в реакции взаимодействия водорода с кислородом на никелевом катализаторе в Институте катализа, явилось первым этапом развития нелинейной динамики в катализе. Установление и признание существования регулярных, квазипериодических и хаотических автоколебаний без случайных источников стало научным открытием в гетерогенном катализе и пусковым механизмом бурного развития нелинейной динамики в катализе. Автоколебания скорости гетерогенной каталитической реакции стали уникальным инструментом, который позволил проникнуть в нелинейную область гетерогенного катализа, ранее трудно доступную.
При анализе теорий автоколебаний и управления динамическими системами академик А.А. Андронов придавал большое значение понятию положительной и отрицательной обратной связи. Обратная связь - это воздействие результатов функционирования системы на характер этого функционирования. Если под воздействием обратной связи первоначальное отклонение от стационарного состояния уменьшается, то говорят, что имеет место отрицательная обратная связь, в противоположном случае говорят о положительной обратной связи. Обычно положительная обратная связь приводит к неустойчивому состоянию каталитической системы в целом, которое обычно очень быстро развивается. Признание существования нелинейных обратных связей в каталитических процессах - это одно из основных эмпирических обобщений изучения каталитических систем.
Открытие автоколебаний скорости гетерогенной каталитической реакции показывает, что корни прогресса заложены в непредсказуемых экспериментальных наблюдениях. Однако, надо понимать, что только подготовленный интеллектуально коллектив сотрудников может извлечь из случайных находок пользу для науки и промышленности.
3. Детерминированный хаос
3.1. Краткая история.
Освобожденный от своего почти мистического смысла хаос должен рассматриваться как еще один вид состояний, отличный от стационарных и упорядоченных состояний. Появление хаоса в детерминированной каталитической системе, в системах другой природы и, особенно, понимание природы случайности, безусловно, является революцией в науке. Потрясение, вызванное этим открытием, аналогично открытию статистических предсказаний в квантовой механике. Научные революции не разрушают существующие знания и являются естественным развитием. Научная революция имеет созидательный характер. Преемственность науки не нарушается. Новые явления рождаются в недрах старых. Сложные, хаотические режимы уже содержались в понятии неинтегрируемые системы. А. Пуанкаре в конце 19 века рассматривал проблему 3х взаимодействующих тел и нашел, что эта система неинтегрируемая.
Возникновение детерминированного хаоса подготовило развитие трех проблем. Это исследование А. Пуанкаре проблемы 3х тел и теоремы о возвращении, гипотеза эргодичности и нелинейные колебания. Неинтегрируемая система не может быть преобразована в систему взаимодействующих частиц, и при больших временах ее поведение непредсказуемо. Закон всемирного тяготения Ньютона, которому подчиняется движение трех тел, является нелинейным и совершенно детерминированным. Однако, отдаленная судьба трех тел может в значительной степени быть зависима от их начального положения и скорости. Это случай детерминированного хаоса. Возникает непредсказуемость на длительном промежутке времени, которая вскрывает природу случайности в детерминированных системах. Случайность и хаотичность становятся важными характеристиками нелинейных каталитических динамических систем. Существенна и теорема А. Пуанкаре о возвращении, которая характеризует поведение консервативной динамической системы. Согласно этой теории, через любую окрестность U любой точки, принадлежащей фазовому пространству, проходит траектория, которая возвращается в окрестность начального состояния U.
Вторая проблема также играет существенную роль в развитии нелинейной динамики. Л. Больцман стремился соединить механику Ньютона со статистической механикой, вывести термодинамические закономерности из уравнений механики. Эргодическая гипотеза, выдвинутая Л. Больцманом в 1887 г. состоит в предположении, что средние по времени значения физических величин, характеризующие консервативную систему, равны средним статистическим. Эргодичность соответствует регулярному квазипериодическому заполнению фазового пространства траекториями. Неустойчивость нелинейной каталитической системы в совокупности с ограниченностью энергии колебаний может вызвать перемешивание фазовых траекторий, которые также приводят к необходимости введения статистического описания. Свойство эргодичности - необходимое, но не достаточное условие хаотичности динамических систем. Перемешивание ведет за собой эргодичность. Перемешивание имеет место тогда, когда в фазовом пространстве близкие в начальный момент времени точки будут разбегаться по сильно расходящимся траекториям (локальная неустойчивость). Оно также ведет к необратимости. Таким образом, перемешивание гораздо более сильное свойство, чем эргодичность.
Развитие теории и практики нелинейных колебаний играло ключевую роль в возникновении и понимании хаотических режимов. Создание современной теории нелинейных колебаний связано с именами математиков А. Пуанкаре, Д. Биркгофа и А. Ляпунова. Приложение развитых ими методов к собственно теории колебаний было сделано в трудах Александра Александровича Андронова (19011952) в школе академика Л.И. Мандельштама.
Академик А.А. Андронов был основателем теории рождения предельных циклов. В 1929 г. на физическом факультете МГУ он защитил диссертацию "Предельные циклы Пуанкаре и теория колебаний". А.А. Андронов выявил глубинную связь физических явлений и математических нелинейных структур.
Он впервые нашел связь между абстрактными предельными циклами Пуанкаре и периодическими колебаниями в ламповом генераторе. Такие колебания он назвал автоколебательными.
В 1930г. на физфаке МГУ был впервые в мире прочитан Л.И. Мандельштамом курс лекций по теории нелинейных колебаний и волн. В Киеве также сложилась школа нелинейных колебаний академиков Н.М. Крылова и Н.Н. Боголюбова. В их книге "Введение в нелинейную механику" (1937 г.) дано строгое математическое обоснование приближенных методов решения нелинейных уравнений. Голландский физик Балтазар Ван Дер Поль (18891959) также внес значительный вклад в теорию нелинейных колебаний. Он работал в фирме "Филипс" и им в 1920 г. было найдено уравнение автоколебаний
d2x/dt2 ε (1x2)dx/dt+x=0
где х координата, ε положительная величина. Пока колебания малы, х2 <1 коэффициент при dx/dt меньше 0, происходит нарастание колебаний - система раскачивается. При возрастании колебаний, если х2 >1, трение становится положительным и уменьшает амплитуду колебаний. В результате движение приближается к режиму автоколебаний с постоянной амплитудой.
Существование непериодических установившихся движений в динамической системе третьего порядка было отмечено в 1963 г. в работе Э. Лоренца. Эдвард Лоренц метеоролог, который работал в Массачусетском технологическом институте, в 1963 г. исследовал атмосферную конвекцию. Он аппроксимировал соответствующие гидродинамические уравнения системой нелинейных обычных дифференциальных уравнений, описывающих ограниченное число мод. Он обнаружил с помощью ЭВМ, что в определенной области параметров, эта система обладает высокой чувствительностью к начальным условиям и описывает хаотическое поведение. Исследуя это явление, он последовательно уменьшал число мод, необходимых для появления хаоса. Оказалось, что хаос возникает при числе мод, равном трем, в противоречии с существующим мнением, что для хаоса необходимо большее число мод. В результате математического моделирования получился объект, который впоследствии был назван аттрактором Лоренца. Фазовая траектория аттрактора Лоренца представляет собой бесконечную линию без самопересечений, причем при t→ ∞ траектория не покидает заданную область и не притягивается ни к точкам равновесия, ни к циклическим траекториям. Сложная хаотическая траектория блуждает между тремя стационарными состояниями: неустойчивым узлом и двумя неустойчивыми предельными циклами. Для хаотической динамики автокорреляционная функция имеет характерный вид. Она экспоненциально спадает с увеличением времени. Высокую чувствительность к начальным условиям Лоренц назвал "Эффектом бабочки". Имя "хаос" дал Джим Йорке - прикладной математик университета Мэриленда в 1975 г.
Рюэль и Такенс в 1971 г. опубликовали статью "О природе турбулентности", где они считали, что турбулентный поток описывается не суперпозицией множества мод (как предполагали Ландау и Хопф), а аттрактором типа Лоренца, который они назвали странным.
Сложные движения в динамической системе были также обнаружены и исследовались на физическом факультете МГУ. Такие движения назывались непериодическими устойчивыми по Пуассону и неустойчивыми по Ляпунову. Эта терминология основывалась на книге В.В. Немецкого и В.В. Степанова "Качественная теория дифференциальных уравнений", вышедшей в 1947 г. Отсутствие ЭВМ в то время не позволило открыть странный аттрактор. Важный вклад в открытие хаотических движений внес в 19581970 гг. своими работами о гомоклинических структурах Ю.К. Неймарк ученик А.А. Андронова. Гомоклиническая траектория - это траектория динамической системы, стремящейся при t → ∞ к одной и той же периодической траектории, либо к одному и тому же положению стационарного состояния. Наличие гомоклинической траектории является критерием стохастичности динамических систем. Большую роль в развитии представлений о хаосе сыграли работы советских математиков Д.В. Аносова, А.И. Колмогорова, Я.Г. Синая; физиков, ученика А.А. Андронова - А.В. Гопонова - Грехова, а также академиков Б.В. Чирикова и Г.М. Заславского.
3.2. Суть хаоса
Хаос характеризуется неповторяющейся, нерегулярной, беспорядочной последовательностью состояний. Детерминированным он называется потому, что хаотическое поведение возникает из совершенно детерминированного закона эволюции каталитической системы. С ростом размерности фазового пространства больше двух, резко усложняется бифуркационная картина - растет число точек бифуркации и, что еще более важно, в каждой точке ветвления рождается все большее количество возможных состояний. В результате мы наблюдаем хаотическое поведение скорости реакции каталитического процесса. Подобные состояния мы называем химической турбулентностью. Для кинетической области целесообразен термин кинетическая турбулентность. Термин турбулентность использован не случайно и имеет глубокий смысл. Возникновение турбулентности - процесс стохастизации изначально ламинарного потока вязкой несжимаемой жидкости в трубе, при возрастании неравновестности, характеризуемой числом Рейнольдса, после его критического значения.
Раньше стохастизацию связывали с возбуждением большого числа мод с неизмеримыми частотами и случайными фазами. В настоящее время стало ясным, что турбулентность возникает при малом числе свобод, а наличие большого числа возбужденных мод не является достаточным условием для возникновения взаимной стохастизации.
Образ детерминированного хаоса связан со странными аттракторами в фазовом пространстве. Особенностью странного аттрактора является экспоненциальная локальная неустойчивость фазовых траекторий и фрактальная нецелая размерность. Первая служит критерием хаотического поведения каталитической системы во времени, а вторая - дробная размерность - свидетельствует о геометрической сложности объекта. Странный аттрактор показывает, сколь причудливыми и запутанными могут быть изменения скорости гетерогенной реакции, если рассматривать процесс одновременно и в прошлом, и в будущем.
Возникновению сложного поведения скорости гетерогенной каталитической реакции предшествует мягкие и жесткие бифуркации регулярных режимов. Необходимо глубокое понимание бифуркационных явлений в каталитической системе, особенно это важно при наличии флюктуаций. Если система неустойчивая, то фазовая траектория изменения состояния будет отличаться от траектории, полученной в результате решения задачи Коши. Поэтому надо одновременно рассматривать не одну траекторию, а весь пучок возможных фазовых траекторий, то есть исследование поведения системы при возможных вариантах начальных условий с учетом флюктуаций. В этом случае возникает трубка фазовых траекторий.
В неустойчивом состоянии отклонения от стационарного состояния быстро нарастают во времени. Однако всегда в системе возникает механизм нелинейного ограничения. Поэтому отклонения будут уменьшаться, и система начнет возвращаться в окрестность неустойчивого состояния, от которого она вновь будет отклоняться. Таким образом, нелинейное ограничение - важнейший элемент возникновения хаоса. Нелинейность - необходимое, но не достаточное условие для возникновения хаотических изменений скорости реакции. Первопричиной нерегулярности является быстрое разбегание первоначально близких фазовых траекторий. Количественной мерой скорости экспоненциального разбегания траекторий служит показатель Ляпунова:
D (t) = D (о) eλt λ=lim 1/τ ln D(+)/D(o)
где D (t)начальное отклонение, λ показатель Ляпунова.
Удивительно, что, несмотря на чрезвычайное разнообразие нелинейных каталитических, химикотехнологических и других динамических систем, механизм возникновения стохастичности осуществляется по небольшому числу путей. Наиболее известны три типовых сценария перехода к хаосу: последовательность бифуркаций удвоения периода цикла (сценарий Фейгенбаума), переход к хаосу через квазипериодические режимы (Рюэля - Такенса) и переход к хаосу через перемежаемость (сценарий Помо - Манневиля). Эти сценарии являются типичными, но возможны и иные сценарии возникновения хаоса.
В 1978 г. М. Фейгенбаум обнаружил универсальный механизм перехода к хаосу, который определяется через бесконечную цепочку удвоения периодического движения. По мере изменения параметра каталитической системы исходный предельный цикл с периодом Т становится неустойчивым - рождается устойчивый цикл с удвоенным периодом. При дальнейшем изменении параметра системы этот цикл также становится неустойчивым - рождается четырехкратный цикл с периодом 4Т. Таких удвоенных периодов в ограниченной области изменения параметров может быть как угодно много. В конечном итоге рождается цикл с бесконечным периодом, происходит хаотизация. Возникает странный аттрактор. Этот механизм перехода к хаосу часто встречается в химических диссипативных системах.
По сценарию Рюэля и Такенса происходит бифуркация устойчивого предельного цикла на плоскости. Он переходит в трехмерный. При этой бифуркации могут образовываться, как незамкнутые, так и замкнутые траектории с двумя независимыми частотами. Незамкнутые траектории заполняют тор. Этот тор также может стать неустойчивым и возникают три независимых частоты. Трехчастотное движение является структурно неустойчивым и возникает странный аттрактор. Изучение спектров Фурье хорошее диагностическое средство анализа динамического поведения каталитической системы.
Механизм Помо - Манневиля, открытый в 1980 г., предполагает чередование регулярного поведения и хаоса. Периодическое движение по предельному циклу может сменяться хаотическим режимом. Этот сценарий называют переходом к хаосу через перемежаемость.
Детерминированный хаос совсем не является экзотическим явлением и, вероятно, встречается много чаще, чем нам представляется. Чем сложнее система, то есть чем больше степеней свободы, и чем выше степень ее неравновестности, тем надежнее устанавливается в ней хаотическое, турбулентное движение. Дело в том, что бывает невозможно сказать, вызвано ли нерегулярное поведение посторонним шумом, экспериментальными ошибками или внутренней динамикой. Природа хаоса такова, что он выглядит подобно стохастическому процессу. В то же время хаос представляет собой, действительно, очень сложную структуру и она может проявляться так, что структура хаоса не может быть вообще распознана. Парадоксально, что чем более неустойчиво ведет себя каталитическая система, тем более точный метод необходим для ее настоящего распознавания. Системы управления могут быть особенно склонны к хаотическому поведению. Хаотическое поведение возникает естественным образом в системах управления вследствие более высокой сложности системы реактор - управляющее устройство. Хаос, обусловленный введением дополнительных переменных, связанных с управлением, затрудняет анализ каталитического процесса. Например, в мире существует более 250 миллионов реакторов - нейтрализаторов выхлопных газов автомобильных двигателей внутреннего сгорания. Регулирование начального состава реакционной смеси вокруг стехиометрического соотношения воздухтопливо создает в нейтрализаторе в ряде случаев хаотический режим.
Хаотическое поведение скорости реакции окисления СО на грани монокристалла платины Pt (110) впервые экспериментально установил Эртл с сотрудниками в 1988 г. Переход к хаосу проходил по сценарию удвоения периода или по сценарию Фейгенбаума. Переход к хаосу через перемежаемость был впервые экспериментально установлен М.М. Слинько, А.А. Ухарским и Н Егерем в 2000 г. при протекании реакции окисления СО на нанесенных палладиево цеолитных катализаторах при атмосферном давлении. Переход был установлен на основе анализа спектров мощности Фурье и сечения Пуанкаре. Перемежаемость выглядит, как изменение периодических колебаний скорости реакции за счет их прерывания хаотическими всплесками. Хаос на палладиево - цеолитных катализаторах возникал вследствие влияния внутренней диффузии на скорость реакции. Это явление получило название - диффузионный хаос.
Диффузионный хаос - это новый тип турбулентности в автоколебательных системах. Вследствие влияния продольной диффузии возможен также хаотический режим в неподвижном слое частиц катализатора. Сложные режимы могут возникать и в проточном реакторе неполного смешения при протекании процессов с нелинейной кинетической моделью.
Хаотические режимы часто наблюдаются при протекании процессов во взвешенном слое катализатора. Взвешенный слой представляет собой открытую сильно нелинейную систему. Хаотические режимы возникают уже при протекании двух последовательных экзотермических реакций. Для более сложных процессов область хаотического режима в реакторе расширяется.
Часто возникают хаотические режимы в реакторах с участием 3х фаз: газ - жидкость - твердый катализатор. Кинетическая турбулентность тесно связана с гидродинамической турбулентностью. Гидрокрекинг в ряде случаев протекает в хаотическом режиме.
Специфической особенностью процессов каталитической полимеризации является то, что динамические характеристики процесса влияют не только на его производительность, но и на качество образующих продуктов. Возникновение автоколебаний, особенно при сополимеризации, может привести к заметному увеличению молекулярной неоднородности образующихся продуктов. Причиной этого может явиться периодическое изменение мгновенного значения состава сополимера в реакторе вследствие самопроизвольного изменения в нем состава мономерной смеси. В этом случае надо избегать автоколебаний, а поэтому возникает задача определений условия их возникновения.
Эпилог
Наше время, а именно, последние 25 лет прошедшего века и век наступивший - может быть охарактеризовано развитием нелинейной динамики каталитических процессов. Открытие автоколебаний скорости гетерогенной каталитической реакции явилось одной из крупных научных сенсаций, вызвавших новое понятие нелинейной физической химии - стохастичность и возникновение структур на всех масштабных уровнях. Фундаментальное значение этих исследований состоит в понимании динамической природы случайности и статистических законов в катализе. Исследования по изучению не нелинейных свойств и нелинейной динамики не видны постороннему взгляду. Однако, они составляют основу, скрытый фундамент учения о катализе.
Наноскопическая нелинейная наука и техника станут основой синтеза катализаторов. Способность работать на молекулярном уровне открывает невероятные перспективы.
Познание нелинейных законов каталитических явлений не было поступательным процессом, на этом пути были заблуждения и недооценка роли нелинейности. Ученые физикохимики избегали темы случайности, неустойчивости и хаотичности. Было стремление описать каталитические явления на основе линейных зависимостей путем сглаживания наблюдаемых сложных явлений. Тем не менее, сейчас они играют центральную роль в нашем понимании каталитических явлений. Принципы современной нелинейной динамики - это та основа, на которой зиждется теория и практика промышленного катализа и, повидимому, зиждется организация жизни на Земле. Нелинейная динамика охватывает каталитический процесс в целом и за большое время. Эти положения более 40 лет лежали в основе деятельности коллектива отдела кинетики и моделирования Института катализа, которые обобщены в книге "Основы и принципы математического моделирования каталитических процессов". Нам представлялось, что основной физикохимической концепцией, определяющей облик нелинейной динамики каталитических процессов, является исследование неустойчивостей стационарных состояний, их дальнейшего развития и стабилизации, с которыми связанно возникновение явлений самоорганизации структур и всех нелинейных явлений и эффектов.
Нелинейная динамика непрерывно повышает наш уровень знания о катализе и степень нашего интеллектуального развития.
М.Г. Слинько
под ред. Р.Л. Бурвелла
Предисловие к русскому переводу
Любая область знания требует использовать язык, достаточно полно и однозначно описывающий интересующие эту область явления. Чем сложнее область знания, тем труднее выбрать подходящий язык и однозначные термины, используемые этим языком.
Катализ - одно из наиболее сложных и комплексных направлений химии вообще и физической химии в частности. язык науки о катализе развивался одновременно с пониманием сути явления катализа, однако и до настоящего момента этот язык нельзя считать окончательно установившимся. Такая недоработанность языка особенно чувствуется в связи с необходимостью достаточно корректной и полной формализации информации о каталитических системах при составлении электронных баз данных и создании систем прогнозирования, то есть того, что, в частности, составляет теоретическую и математическую основу недавно появившегося направления, объединяемого терминами"комбинаторный катализ" или, что более верно,"высокопроизводительные ("high throughput") методы поиска катализаторов".
Следует признать, что катализ оказался весьма"обделенным" вниманием ИЮПАК -Международного союза чистой и прикладной химии, занимающегося проблемами терминологии в различных областях химии.
Последняя известная нам (и совсем уже неизвестная молодежи) последовательная попытка систематизации терминологии в катализе была проделана еще в 1975 году под руководством профессора Р. Бурвелла, объединившего под эгидой ИЮПАК большую группу известных специалистов в катализе [1] (дубль этой работы опубликован в [2]). С советской стороны в работе группы активное участие принимали Г.К. Боресков и В.Б. Казанский. Безусловно, четверть столетия, прошедшая с момента публикации [1, 2], требует внесения в указанные рекомендации определенных коррекций и дополнений. Однако несомненно, что уже существующие рекомендации ИёПАК должны быть использованы в качестве базиса для дальнейшего уточнения используемой в катализе терминологии.
В связи с тем, что публикации [1, 2] оказались малоизвестными отечественным специалистам и, более того, по большому недоразумению не был сделан их своевременный перевод на русский язык, мы публикуем в"Каталитическом бюллетене" как оригинальный английский текст работы [1, 2], так и его перевод на русский язык, любезно сделанный Е.Б. Никифоровой.
Мы уверены в том, что такая публикация будет полезна не только тем, кто лишь недавно вступил в ряды активно работающих химиков-каталитиков, но и опытным специалистам, заинтересованным в использовании однозначных и хорошо отработанных терминов.
Хотелось бы надеяться, что читатели"Каталитического бюллетеня" активно продолжат обсуждение данного вопроса в Бюллетене.
Редактор русского перевода
В. Пармон
Литература
1.1 Катализ и катализаторы
Катализ - это явление, в котором инородный материал, названный катализатором, присутствуя в относительно малом количестве и не расходуясь, увеличивает скорость химической реакции. То же относится к реагентам, для которых добавление некоторого вещества уменьшает скорость определенной реакции, например введение ингибитора в цепную реакцию или яда в каталитическую реакцию. Термин "отрицательный катализ" использовался для описания этих явлений, но теперь он не рекомендуется; предпочтительными являются такие термины, как ингибирование или отравление.
Катализатор обеспечивает протекание ряда элементарных процессов (часто называемых элементарными стадиями), которые связывают реагенты и продукты реакции и которые не протекают в отсутствие катализатора. Например, предположим, что реакция
А = С
идет с некоторой скоростью, которая может быть измеримой, но может быть близкой к нулю. Добавление Х может обеспечить новый маршрут, включающий интермедиат В,
|
А + Х |
|
|
В |
|
Если реакция идет по этому маршруту со скоростью, значительной по сравнению со скоростью некатализируемой реакции, так что суммарная скорость возрастает, то Х - катализатор. В этом смысле каталитическая реакция - это замкнутая последовательность элементарных стадий, подобная стадиям продолжения газофазной цепной реакции.
Катализатор вступает в реакцию, но регенерируется в конце каждого реакционного цикла. Таким образом, одна единица катализатора обеспечивает конверсию многих единиц реагентов (но см. §1.7).
Конечно, катализатор может ускорять только одну или некоторые из нескольких термодинамически возможных реакций.
Трудно разделить природу на отдельные составляющие и, вероятно, ни одно из рабочих определений катализа не может быть полностью удовлетворительным. Так, вода может облегчить реакцию между двумя твердыми веществами, растворяя их. Это явление может казаться примером катализа, но такой эффект растворителя, в общем случае, не рассматривается в рамках катализа. Кинетический солевой эффект в растворе также обычно исключается из рассмотрения. Далее, катализатор должен быть веществом и, несмотря на то, что подвод теплоты к системе обычно увеличивает скорость реакции, теплоту не называют катализатором, также как и свет, вызывающий реакцию между хлором и водородом, не является катализатором.
Следует различать катализатор и инициатор. Инициатор начинает цепную реакцию, например, перекись ди-т-бутила в полимеризации стирола, но инициатор расходуется в реакции. Это не катализатор.
В гомогенном катализе все реагенты и катализатор молекулярно диспергированы в одной фазе.
В гетерогенном катализе катализатор образует отдельную фазу. Обычно катализатор является кристаллическим или аморфным твердым веществом, тогда как реагенты и продукты находятся в одной или более жидких фазах. Каталитическая реакция идет на поверхности твердого вещества и, в идеале, ее скорость пропорциональна поверхности катализатора. Однако на практике скорость может ограничиваться транспортными процессами (см. §1.6).
Большинство примеров катализа легко различаются как гомогенные и гетерогенные, но некоторые находятся на пересечении этих двух типов. Рассмотрим систему, в которой интермедиаты образуются на поверхности, а затем десорбируются в газовую фазу. Такие интермедиаты могут генерировать цепную реакцию в газовой фазе, т.е. инициация и обрыв цепи происходят на поверхности, но рост цепи - в газовой фазе.
Катализ ферментами может обладать некоторыми характеристиками как гомогенного, так и гетерогенного катализа, когда катализатором является макромолекула, которая достаточно мала, чтобы быть молекулярно диспергированной в одной фазе со всеми реагентами, но достаточно велика, чтобы говорить об активных центрах на ее поверхности.
Данное руководство посвящено гетерогенному катализу. Другие типы катализа далее не будут рассматриваться.
1.2 Адсорбция
1.2.1 Общие термины
Несмотря на то, что адсорбция существует как объект научных исследований, независимый от ее роли в гетерогенном катализе, она требует особого внимания в рамках данного руководства, благодаря ее определяющей роли в гетерогенном катализе. Большинство или почти все каталитические реакции включают адсорбцию по крайней мере одного из реагентов. Многим терминам, относящимся к адсорбции, уже были даны определения в Приложении II, Части I, §1.1. (Справочник символов и терминологии по физико-химическим величинам и единицам, подготовленный ранее комиссией по коллоидной и поверхностной химии, IUPAC) Они включают поверхность, поверхность раздела, площадь поверхности или поверхности раздела и удельную площадь поверхности. Приложение II, Часть I рекомендует A или S и a или s как обозначения, соответственно, площади поверхности и удельной площади поверхности. As и as могут использоваться там, где это необходимо, во избежание путаницы с энергией Гельмгольца A или энтропией S.
Другими терминами являются сорбция, сорбтив и сорбат [различая вещество в сорбированном состоянии (сорбат) и вещество в текучей фазе, которое может быть сорбировано (сорбтив)], абсорбция, абсорбтив, абсорбат, абсорбент; и адсорбция, адсорбтив, адсорбат, адсорбент(Использование термина субстрат для обозначения адсорбента или носителя должно обескураживать, так как обычно используется в химии ферментов для обозначения реагентов) . Термин адсорбированный комплекс используется для обозначения объекта, образованного адсорбатом и той частью адсорбента, с которой он связан.
Приложение II, Часть I, §1.1.5 следующим образом рассматривает поверхность раздела адсорбент/флуид (подвижная среда) (ПРиложение II, Часть I рекомендует. Косая черта предпочтительнее, чем дефис, для разделения названий объемных фраз, т.к. использование дефиса может привести к двусмысленности) . "Зачастую полезно рассматривать поверхность раздела адсорбент/флуид как содержащую две области. Область флуидной (текучей) фазы (т.е. жидкость или газ) как часть этой поверхности раздела может быть названа областью адсорбции, тогда как часть адсорбента, включенная в поверхность раздела, называется поверхностным слоем адсорбента".
Для процесса, в котором молекулы* или диссоциированные молекулы накапливаются в адсорбционном пространстве или в приповерхностном слое абсорбента, термином, противопоставленным адсорбции, будет десорбция, обозначающая обратный процесс (см. Приложение II, Часть I, §1.1.4). Адсорбция также используется для обозначения результата процесса адсорбции, т.е. присутствия адсорбата на адсорбенте. Адсорбированное состояние может быть или не быть в равновесии с адсорбтивом [см. 1.2.2(с)].
Адсорбция и десорбция также указывают направление достижения равновесия, например, кривая (точка) адсорбции, кривая (точка) десорбции.
1.2.2 Хемосорбция и физосорбция
Соответствующие фрагменты §§1.1.6 и 1.1.7 Приложения II, Части I приведены ниже.
"Хемосорбция и физосорбция"
Хемосорбция (или химическая адсорбция) - это адсорбция, в которой действуют такие же валентные силы, как и при образовании химических соединений. Разграничение хемосорбции и физосорбции является, по сути, проблемой, сходной с разграничением химического и физического взаимодействия вообще. Абсолютно четкое различие невозможно; существуют промежуточные случаи, например, адсорбция, включающая сильные водородные связи или слабый перенос заряда.
Отличить хемосорбцию можно по некоторым признакам, в том числе следующим:
Физосорбция (или физическая адсорбция) - это адсорбция, при которой действуют те же межмолекулярные силы (силы Ван дер Ваальса), что и силы, отвечающие за неидеальность реальных газов и конденсацию паров, и которые не вызывают существенные изменения электронных орбиталей адсорбированных молекул. Термин Ван дер Ваальсова адсорбция, хотя и является синонимом термина физическая адсорбции, для использования не рекомендуется.
Распознать физическую адсорбцию можно по некоторым признакам, в том числе:
Монослойная и многослойная адсорбция, заполнение микропор и капиллярная конденсация
При монослойной адсорбции все адсорбированные молекулы находятся в контакте с поверхностным слоем адсорбента.
При многослойной адсорбции адсорбционное пространство содержит более одного слоя молекул, и не все адсорбированные молекулы находятся в контакте с поверхностным слоем адсорбента.
Монослойной емкостью называют в случае хемосорбции количество адсорбата, необходимое для заполнения всех адсорбционных центров, определяемых структурой адсорбента и химической природой адсорбтива, а в случае физосорбции - количество адсорбата,
необходимое для покрытия поверхности заполненным монослоем молекул в плотной упаковке, причем плотная упаковка при необходимости должна быть явно выражена. Величины, относящиеся к монослойной емкости, могут обозначаться подстрочным индексом m.
Покрытие поверхности(q ), в случае как монослойной, так и многослойной адсорбции, определяется как отношение количества адсорбированного вещества к монослойной емкости.
Площадь, занимаемая одной молекулой в заполненном монослое, обозначается am; например, для молекул азота am (N2).
Заполнение микропор - это процесс, в котором молекулы адсорбируются в адсорбционном пространстве внутри микропор.
Объем микропор обычно измеряется по объему адсорбированного материала, заполняющего микропоры полностью, и выражается в единицах объема жидкости при атмосферном давлении и температуре измерений.
В определенных случаях (например, пористые кристаллы) объем микропор может быть найден из структурных данных.
Говорят, что в пористых твердых телах имеет место капиллярная конденсация, когда полимолекулярная адсорбция из газовой фазы происходит до точки, в которой пористое пространство заполнено жидкостью, отделенной менисками от газовой фазы.
Понятие капиллярной конденсации теряет смысл, когда размеры пор настолько малы, что термин "мениск" уже не имеет физического смысла. Капиллярная конденсация часто сопровождается гистерезисом."
1.2.3 Типы хемосорбции
Недиссоциативная и диссоциативная хемосорбция. Если молекула адсорбируется без фрагментирования, то адсорбционный процесс является недиссоциативным. К такому типу часто относится адсорбция моноокиси углерода. Если адсорбируемая молекула диссоциирует на два или более фрагментов, оба или все из которых связаны с поверхностью адсорбента, такой процесс называется диссоциативным. Хемосорбция водорода относится преимущественно к такому типу.
H2(g)  2H (ads) или H2(g) + 2*
2H (ads) или H2(g) + 2* 2H*
2H*
Звездочка обозначает поверхностный центр.
Термины гомолитический и гетеролитический относятся обычно к формальной природе разрыва одинарной связи. Если в процессе диссоциативной адсорбции электронная пара химической связи адсорбтива А : В разделяется, то это гомолитическася диссоциативная адсорбция. Если же электронная пара остается у А или В, то говорят о гетеролитической диссоциативной адсорбции.Ниже даны примеры.
(а) Гомолитическася диссоциативная адсорбция водорода на поверхности металла:
H2 + 2* 2H*.
2H*.
(b) Гетеролитическая диссоциативная адсорбция водорода на поверхности оксида, в котором для поверхностных центров Mn+ и O2 - характерна более низкая координация, чем для ионов в объеме фазы:
H2 + Mn+ + O2 -  H - Mn+ + HO - .
H - Mn+ + HO - .
При необходимости внесения еще большей определенности это уравнение может быть записано как
H2(g) + Msn+ + Os2 -  H - Msn+ + HOS - ,
H - Msn+ + HOS - ,
где подстрочный индекс s указывает на то, что данные группы принадлежат поверхности.
Обозначение H - Mn+ используется, как и в традиционной терминологии неорганической химии, для указания сохранения степени окисления М.
(c) Гетеролитическая диссоциативная адсорбция воды на такой же паре центров, как и в примере (б):
H2O + Mn+ + O2 -  HO - Mn+ + HO - .
HO - Mn+ + HO - .
Восстановительная и окислительная диссоциативная адсорбция аналогичны терминам, используемым в координационной химии, которые, например, описывают следующую реакцию как окислительное присоединение
L4M(I) + H2  L4M(III)H2.
L4M(III)H2.
Здесь М - атом переходного металла, а L - лиганд. Н как лиганд дан в степени окисления - 1. При восстановительном присоединении электронная пара, образующая связь в сорбтиве А : В, переносится к поверхностным соединениям; в случае окислительного присоединения электронная пара удаляется из поверхностных соединений. Можно сказать, что диссоциативная адсорбция Cl2 на металле является окислительной, если на поверхности адсорбента хлор образует ионы Cl - . Диссоциативная адсорбция будет восстановительной, если, например, идет таким образом:
H2(g) + 2[M(III)O2 - ]s  2[M(II)(OH) - ]s.
2[M(II)(OH) - ]s.
Заметим, что здесь H2  2H+ + 2e.
2H+ + 2e.
Адсорбция с переносом заряда - это разновидность окислительной или восстановительной хемосорбции, в которой слова "восстановительная" или "окислительная" относятся к приобретению или потере электрона группами твердого тела. В простых случаях она недиссоциативна, т.е. происходит просто перенос заряда между адсорбривом и адсорбентом с образованием адсорбата. Ниже даны два примера.
pВосстановительная: X + *  X+* -
X+* -
где Х - ароматическая молекула с низким потенциалом ионизации, такая как антрацен или трифениламин, а * - центр на алюмосиликате.
Окислительная: О2 + *  О2 - * +
О2 - * +
Термин "адсорбция с переносом заряда" применялся также к адсорбции, напоминающей комплексы Малликена с переносом заряда.
Иммобильный, мобильный. Эти термины используются для описания свободы перемещения молекул адсорбата по поверхности. Адсорбция называется иммобильной, когда значение kT меньше величины D E энергетического барьера, разделяющего близлежащие центры. В этом случае у адсорбата мало возможности мигрировать по соседним центрам, и такая адсорбция обязательно локализованная. Подвижность адсорбата будет возрастать с повышением температуры, и мобильная адсорбция может быть как локализованной, так и нелокализованной. В случае локализованной мобильной адсорбции адсорбат основное время находится на адсорбционных центрах, но может мигрировать или десорбироваться с последующей реадсорбцией на других местах. При нелокализованной адсорбции подвижность настолько велика, что лишь малая часть адсорбированных групп находится на адсорбционных центрах, в то время как большая часть находится на других местах поверхности.
В некоторых случаях локализованной адсорбции адсорбат упорядочен в двумерную решетку или сеть в некоторой области значений покрытия поверхности и температур. Если сеть упорядоченной адсорбированной фазы соответствует решетке адсорбента, то структуру называют когерентной, в противном случае это некогерентная структура (см. также §2.4).
Каждому из типов процессов адсорбции может соответствовать десорбция в обратной форме, например процесс, обратный диссоциативной адсорбции - это ассоциативная десорбция. Тем не менее, процесс хемосорбции может быть и необратимым [§1.2.2(с)]. В результате десорбции могут образовываться соединения, отличные от адсорбированных, например, при десорбции этана, диссоциативно адсорбированном на чистом никеле, очень мало или вообще не образуется этан; 1-бутен, диссоциативно адсорбированный на окиси цинка с образованием метилаллила и Н, дает при десорбции 2-бутены, а с поверхности вольфрама, покрытой адсорбированным кислородом, может испаряться WO3.
Фотоадсорбция, фотодесорбция. Световое излучение (обычно в видимой или ультрафиолетовой областях) может воздействовать на адсорбцию. В системе, содержащей адсорбтив и адсорбент, воздействие света может приводить к увеличению адсорбции (фотоадсорбция) или к десорбции адсорбата (фотодесорбция).
1.2.4 Центры хемосорбции
Классификация центров может производиться исходя из их химической природы в соответствии с обычной химической терминологией. Следующие термины являются простым расширением области обычного использования химических терминов: оснoвные центры ,кислотные центры льюисовские кислотные центры,протонные или бренстедовские кислотные центры,электроноакцепторные центры и электроннодонорные центры (два последних примера могут возникать в связи с адсорбцией с переносом заряда).
Нередко полезно учитывать, что центры хемосорбции являются результатом координационной ненасыщенности поверхности, т.е. того, что координационное число поверхностных атомов меньше координационного числа таких же атомов в объеме. Так, например, ион хрома на поверхности окиси хрома имеет координационное число меньшее, чем ион хрома в объеме. Поэтому этот ион хрома будет стремиться к образованию связи с подходящим адсорбтивом, чтобы восстановить свое координационное число. Координационное число атома, находящегося на плоскости (100) гранецентрированного кубического металла, равно 8 по сравнению с числом 12 для атома в объеме металла; это тоже является примером координационной ненасыщенности поверхности. Однако, конечно, существуют центры, к которым понятие поверхностной координационной ненасыщенности неприменимо, например, это бренстедовские кислотные центры.
Зачастую нельзя с уверенностью идентифицировать тип и структуру центров в адсорбции и гетерогенном катализе. Однако для теоретического рассмотрения возможных центров необходимо введение ряда обозначений. С одной стороны, хотелось бы иметь возможность использовать общее и неспецифическое описание. Для этого можно порекомендовать символы * и (ads), например, H* и H(ads). С другой стороны, может возникнуть желание использовать как можно более определенные обозначения. В этом случае могут оказаться полезными общехимические символы. Набор символов для металлов включает Cj и Bn, где Cj обозначает поверхностный атом, имеющий j ближайших соседей, а Bn - ансамбль из n поверхностных атомов, которые в совокупности образуют адсорбционный центр, например, адсорбционный центр между тремя поверхностными атомами, образующими углы равностороннего треугольника, является центром типа B3 [более подробно см. van Hardeveld and Hartog, Surface Sci. 15, 189(1969)].
Известны случаи хемосорбции, когда при высокой степени покрытия сеть (двумерная решетка) адсорбата не совпадает с решеткой адсорбента. В таком случае понятие центров с точной локализацией и их фиксированным количеством может оказаться неприменимым. Схожие проблемы в определении центров возникают и в случае перестройки поверхности при взаимодействии адсорбата с адсорбентом. Из-за трудностей, нередко возникающих при определении типа поверхностных центров, часто становится удобным, особенно для металлов, определять покрытие поверхности q как отношение числа адсорбированных атомов или групп к числу поверхностных атомов (сравни §1.2.2).
1.2.5 Однородность центров
Природа центров адсорбции или катализа может меняться даже в случае чистых металлов, где не возникает вопроса относительно различий химического состава той или другой части поверхности. Такие изменения возникают не только вследствие дефектов на поверхности металла, но и потому, что природа центра зависит от структуры поверхности. Однородные центры скорее всего встречаются, когда адсорбция или катализ изучаются на индивидуальной грани монокристалла; тем не менее даже индивидуальные грани могут содержать более одной разновидности центров. Неоднородные центры будут наблюдаться, в качестве нормального явления, в образцах металлов с более чем одним типом доступных кристаллических граней. Различают два вида неоднородности. Собственная неоднородность обусловлена только природой адсорбента. Наведенная(индуцированная) неоднородность возникает в том случае, когда присутствие молекулы адсорбата на одном из центров приводит к изменению силы адсорбции на соседних центрах. Таким образом, совокупность однородных центров на индивидуальной кристаллической грани может стать неоднородной в случае частичного заполнения поверхности хемосорбированными частицами.
При исследовании каталитических свойств металлов важность неоднородности центров зависит от особенностей изучаемой реакции. Для некоторых реакций активность металлического катализатора зависит только от суммарного количества доступных центров; эти реакции называются структурно-нечувствительными. В других реакциях, относящихся к структурно-чувствительным, активность может быть намного выше на центрах, связанных с определенной кристаллической гранью или даже с некоторыми типами структурных дефектов. Для обозначения структурно-нечувствительных и структурно-чувствительных реакций использовались также альтернативные термины легкие и затрудненные реакции, соответственно. Термины в §1.2.5 обсуждались в отношении к поверхности металлов, тем не менее их можно использовать и по отношению к другим адсорбентам и катализаторам, особенно к парным центрам, участвующим в гетеролитической диссоциативной адсорбции.
1.2.6 Активные места, активные центры (Active site, active centre
Термин активные места (active sites) зачастую применяется к центрам адсорбции, являющимся эффективными местами определенной гетерогенной каталитической реакции. Термины активные места и активные центры(active site и active centre) часто используются как синонимы, но термин активный центр может применяться также и для описания ансамбля мест (sites), на которых протекает каталитическая реакция.
1.2.7 Изотермы адсорбции
Изотерма адсорбции простого газообразного адсорбтива на твердом теле является функцией, связывающей при постоянной температуре количество вещества, адсорбированного в равновесии с давлением (или концентрацией) адсорбтива в газовой фазе. Величиной, доступной для экспериментальных измерений, является скорее поверхностный избыток, а не адсорбированное количество, тем не менее при низких давлениях разница между этими двумя величинами становится пренебрежимо малой (см. Приложение II, Часть I, §1.1.11).
Аналогичным образом, когда два или более адсорбтива конкурируют за адсорбцию на поверхности, изотерма адсорбции адсорбтива i при данной температуре есть функция равновесных парциальных давлений адсорбтивов всех типов. В случае адсорбции из жидкого раствора изотерма адсорбции любого преимущественно адсорбированного вещества из раствора может быть определена сходным образом c помощью равновесной концентрации соответствующего компонента раствора, однако изотерма обычно зависит от природы растворителя и от концентраций (мольных долей) других растворенных компонентов, если они есть. Индивидуальные изотермы растворенных веществ не могут быть выведены из поверхностных избытков иначе как с использованием соответствующей модели адсорбированного слоя; когда имеет место хемосорбция, в общем случае можно предположить, что адсорбция монослойная. Количества адсорбированного вещества часто выражаются через степень покрытия q i. В случае хемосорбции q i - это доля центров адсорбции, покрытых веществом i. Ниже описаны типы изотерм адсорбции, представляющие интерес для гетерогенного катализа. Линейная изотерма адсорбции. Простейшая изотерма адсорбции является аналогом закона Генри. В случае единственного адсорбтива она принимает вид
q = Kp или q = Kc,
где p и c - давление и концентрация адсорбтива, q - покрытие адсорбатом, а K - константа равновесия линейной изотермы адсорбции или константа Генри. Большинство изотерм адсорбции сводятся к закону Генри, когда p или c становятся достаточно малыми при условии, что имеет место простая адсорбция, т.е. адсорбция не является ни диссоциативной, ни ассоциативной. То есть при достаточно малом покрытии закон Генри обычно применяется лишь к первому из последующих уравнений, но не ко второму или третьему.
A + * 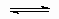 A*;
A*;
A2 + 2* 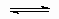 2A*;
2A*;
2A + * 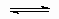 A2*.
A2*.
Изотерма адсорбции Лэнгмюра,
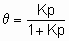 or
or 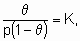
или ее эквиваленты в терминах концентраций обычно имеют место при простой (недиссоциативной) адсорбции из идеального газа на поверхности с фиксированным числом однородных центров, которые могут быть заняты одним, и только одним видом адсорбата. K называется константой равновесия адсорбции по Лэнгмюру. Кроме того, энтальпия адсорбированной формы не должна зависеть от того, заняты или нет соседние центры адсорбции, и, следовательно, энтальпия адсорбции не зависит от q
. Вторая из приведенных выше форм изотермы Лэнгмюра подчеркивает, что константа K является константой равновесия реакции A + * 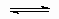 A*. Поскольку постоянство энтальпии при любом покрытии поверхности аналогично постоянству энтальпии при изменении давления идеального газа, адсорбционное состояние в системе, подчиняющейся изотерме адсорбции Лэнгмюра, иногда называют идеальным адсорбционным (адсорбированным) состоянием В случае диссоциативной хемосорбции,
A*. Поскольку постоянство энтальпии при любом покрытии поверхности аналогично постоянству энтальпии при изменении давления идеального газа, адсорбционное состояние в системе, подчиняющейся изотерме адсорбции Лэнгмюра, иногда называют идеальным адсорбционным (адсорбированным) состоянием В случае диссоциативной хемосорбции,
A2 + 2* 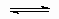 2A*
2A*
уравнение Лэнгмюра принимает вид
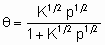 или
или 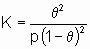
Для простой адсорбции двух адсорбтивов A и B, конкурирующих за одни и те же центры, изотерма Лэнгмюра принимает вид
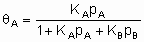 ,
,
где KA и KB - константы равновесия раздельной адсорбции А и В, соответственно. Это уравнение может быть обобщено на случай описания адсорбции нескольких адсорбтивов и может учитывать диссоциативную адсорбцию одного и более адсорбтивов.
В изотерме адсорбции Фрейндлиха количество адсорбированного вещества пропорционально дробной степени давления адсорбтива. В некоторых системах дробная степень и константа пропорциональности являются функциями температуры. С учетом покрытия изотерма принимает вид
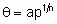 ,
,
где n - число, большее единицы, и a - константа. В области справедливости изотермы (дифференциальная) энтальпия адсорбции является линейной функцией от ln q .
В изотерме адсорбции Темкина количество адсорбированного вещества соотносят с логарифмом давления адсорбтива
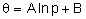 ,
,
где A и B константы. В области справедливости такой изотермы (дифференциальная) энтальпия адсорбции является линейной функцией q . Изотерма адсорбции Брунауера-Эммета-Теллера применима только к физосорбции паров, но важна также и для гетерогенного катализа, поскольку используется для определения поверхности твердых тел. Изотерма описывается следующим уравнением
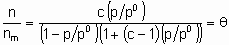 ,
,
где с - константа, зависящая от температуры и природы адсорбтива и адсорбента, n - количество адсорбированного вещества, nm - емкость монослоя и p0 - давление насыщенных паров жидкого адсорбтива при температуре исследования. В соответствии с этим уравнением, основанным на модели многослойной адсорбции, q
превышает единицу, если отношение 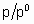 достаточно велико.
достаточно велико.
1.2.8 Бифункциональный катализ
Некоторые гетерогенные каталитические реакции протекают как последовательность элементарных процессов, определенная часть которых локализуется на центрах одного типа, тогда как другие - на центрах совершенно другой природы. Например, некоторые из реакций процесса риформинга углеводородов на катализаторах платина/оксид алюминия протекают на поверхности платины, а другие - на кислотных центрах оксида алюминия. О таких каталитических реакциях говорят как о бифункциональном катализе. Оба типа центров обычно перемешаны в одной и той же первичной частице (§1.3.2), однако те же реакции могут идти даже при использовании смеси частиц, каждая их которых содержит только один тип центров. Такой подход, конечно, может быть расширен, чтобы создать понятие полифункционального катализа.
1.2.9 Скорости адсорбции и десорбции
Коэффициент прилипания - это отношение скорости адсорбции к скорости соударений адсорбтива со всей поверхностью, т.е. как заполненной, так и не заполненной. Обычно это функция покрытия поверхности, температуры и деталей структуры поверхности адсорбента. Вероятность прилипаниячасто используется в таком же смысле, но, в принципе, это микроскопическая величина, относящаяся к процессу индивидуального столкновения. Таким образом, коэффициент прилипания можно рассматривать как среднюю вероятность прилипания, усредненную как по всем углам и энергиям ударяющихся молекул, так и по всей поверхности.
Среднее время задержки (пребывания) адсорбированных молекул - это среднее время, в течение которого молекула остается на поверхности адсорбента, т.е. средний интервал времени между ударом и десорбцией. В то время, когда молекула остается на поверхности, до десорбции она может мигрировать между адсорбционными центрами по поверхности. Если время задержки адсорбированных групп относится к определенным адсорбционным центрам, его можно называть средним временем жизни определенного адсорбционного комплекса. Когда скорость десорбции имеет первый порядок по покрытию, время пребывания не зависит от покрытия поверхности и обратно пропорционально константе скорости процесса десорбции. В этом случае оно также может быть однозначно определено с помощью времени полураспада (полужизни) или какого-либо другого дробного времени жизни десорбционных процессов. Если процесс десорбции не является процессом первого порядка, например, из-за взаимовлияния адсорбированных молекул и/или энергетической неоднородности поверхности, время пребывания зависит от покрытия поверхности, и рабочая формулировка "времени пребывания" требует более конкретного определения.
Неактивированная и активированная адсорбция. Если температурный коэффициент скорости адсорбции очень мал, говорят о неактивированном процессе адсорбции (т.е. имеющем пренебрежимо малую энергию активации). В этом случае коэффициент прилипания при низком покрытии может быть близок к единице, особенно для молекул меньшего размера. Если температурный коэффициент скорости адсорбции имеет существенную величину, то говорят, что процесс - активированный (т.е. имеющий значительную энергию активации). В этом случае коэффициент прилипания мал. В общем случае, энергия активации активированной адсорбции является функцией покрытия и, как правило, возрастает с увеличением покрытия.
Предположены различные соотношения между скоростью активированной адсорбции и покрытием. Особенно часто используют одно из них, а именно уравнение Рогинского-Зельдовича, иногда называемое также уравнением Еловича,
где q - это покрытие, а a и b - константы, характерные для конкретной системы.
1.1 Catalysis and catalysts
Catalysis is the phenomenon in which о relatively small amount of о foreign material, called о catalyst, augments the rate of о chemical reaction without itself being consumed. Cases occur with certain reactants in which the addition of о substance reduces the rate of о particular reaction, for example, the addition of an inhibitor in о chain reaction or о poison in о catalytic reaction. The term "negative catalysis" has been used for these phenomena but this usage is not recommended; terms such as inhibition or poisoning are preferred.
A catalyst provides for sets of elementary processes (often called elementary steps) which link reactants and products and which do not occur in the absence of the catalyst. For example, suppose the reaction
A=C
to proceed at some rate which might be measurable but might be essentially zero. The addition of у might now provide о new pathway involving the intermediate с,
|
А + Х |
|
|
В |
|
If reaction by this pathway proceeds at о rate significant with respect to the uncatalysed rate such that the total rate is increased, у is о catalyst. In this sense, о catalytic reaction is о closed sequence of elementary steps similar to the propagation steps of о gas-phase chain reaction.
The catalyst enters into reaction but is regenerated at the end of each reaction cycle. Thus, one unit of catalyst results in the conversion of many units of reactants (but see Я1.7).
ю catalyst, of course, may catalyse only one or some of several thermodynamically possible reactions.
It is difficult to separate Nature into water-tight compartments and probably no operational definition of catalysis can be entirely satisfactory. Thus, water might facilitate the reaction between two solids by dissolving them. This phenomenon might appear to constitute an example of catalysis but such solvent effects are not, in general, considered to fall within the scope of catalysis. The kinetic salt effect in solution is also usually excluded. Further, о catalyst must be material and, although an input of heat into о system usually augments the rate of о reaction, heat is not called о catalyst, nor is light о catalyst in leading to reaction between chlorine and hydrogen.
ю catalyst should be distinguished from an initiator. An initiator starts о chain reaction, for example, di-t-butylperoxide in the polymerisation of styrene, but the initiator is consumed in the reaction. It is not о catalyst.
In homogeneous catalysis, all reactants and the catalyst are molecularly dispersed in one phase.
In heterogeneous catalysis, the catalyst constitutes о separate phase. In the usual case, the catalyst is о crystalline or amorphous solid, the reactants and products being in one or more fluid phases. The catalytic reaction occurs at the surface of the solid and, ideally, its rate is proportional to the area of the catalyst. However, in practical cases, transport processes may restrict the rate (see §1.6).
Most examples of catalysis can be readily characterised as homogeneous or heterogeneous but there are examples of catalysis which overlap the two types. Consider о system in which intermediates are formed at the surface and then are desorbed into the gas phase and react there. Such intermediates might generate о chain reaction in the gas phase, i.Х., chain initiation and chain termination occur at the surface but chain propagation occurs in the gas phase.
Enzime catalysis may share some of the characteristics of homogeneous and heterogeneous catalysis, as when the catalyst is о macromolecule small enough to be molecularly dispersed in one phase with all reactants but large enough so that one may speak of active sites on its surface.
This manual deals with heterogeneous catalysis. Other types of catalysis will receive ЮЭ further attention.
1.2 Adsorption
1.2.1 General terms
Although adsorption exists as о subject of scientific investigation independent of its role in heterogeneous catalysis, it requires particular attention here because of its central role in heterogeneous catalysis. Most or all catalytic reactions involve the adsorption of at least one of the reactants. Many terms related to adsorption have already been defined in Appendix II, Part I, §1.1. These include surface,interface,area of surface or interface , and specific surface area. Appendix II, Part I, recommends ю or S and о or s as symbols for area and specific area, respectively. ,s and оs may be used to avoid confusion with Helmholtz energy , or entropy S where necessary.
Other terms are sorption, sorptive, sorbate [о distinction being made between о species in its sorbed state (sorbate) and о substance in the fluid phase which is capable of being sorbed (sorptive)], absorption, absorptive, absorbate (The use of substrate for adsorbent or support is to be discouraged because of its general use in enzyme chemistry to designate a reactant) , absorbent; and adsorption, adsorptive, adsorbate, adsorbent. The term adsorption complex is used to denote the entity constituted by the adsorbate and the part of the adsorbent to which it is bound.
Appendix II, Part I, §1.1.5, treats the adsorbent/fluid (Appendix11, Part1, recommendes: The use of a solidus to separate the names of bulk phases is prefereed to the use of a hyphen with can lead to ambiguities) interface as follows. "It is often useful to consider the adsorbent/fluid interface as comprising two regions. The region of the fluid phase (i.Х., liquid or gas) forming part of the adsorbent/fluid interface may be called the adsorption space, while the portion of the adsorbent included in the interface is called the surface layer of the adsorbent."
When used to denote the process in which molecules or dissociated molecules accumulate in the adsorption space or in the surface layer of the absorbent, adsorption has as its counterpart the term desorption which denotes the converse process (see Appendix II, Part I, §1.1.4). Adsorption is also used to denote the result of the process of adsorption, i.Х., the presence of adsorbate on an adsorbent. The adsorbed state may or may not be in equilibrium with the adsorptive [see §1.2.2(c)].
Adsorption and desorption may also be used to indicate the direction from which equilibrium has been approached, Х.g., adsorption curve (point), desorption curve (point).
1.2.2 Chemisorption and physisorption
For convenience, the relevant portions of §§1.1.6 and 1.1.7 of Appendix II, Part I, are reproduced here.
"Chemisorption and physisorption
Chemisorption (or Chemical Adsorption) is adsorption in which the forces involved are valence forces of the same kind as those operating in the formation of chemical compounds. The problem of distinguishing between chemisorption and physisorption (see below) is basically the same as that of distinguishing between chemical and physical interaction in general. No absolutely sharp distinction can be made and intermediate cases exist, for example, adsorption involving strong hydrogen bonds or weak charge- transfer.
Some features which are useful in recognising chemisorption include:
(о) the phenomenon is characterised by chemical specificity;
(b) changes in the electronic state may be detectable by suitable physical means (Х.g., u.v., infrared or microwave spectroscopy, electrical conductivity, magnetic susceptibility);
(c) the chemical nature of the adsorptive(s) may be altered by surface dissociation or reaction in such о way that on desorption the original species cannot be recovered; in this sense chemisorption may not be reversible;
(d) the energy of chemisorption is of the same order of magnitude as the energy change in о chemical reaction between о solid and о fluid: thus chemisorption, like chemical reactions in general, mоб be exothermic or endothermic and the magnitudes of the energy changes may range from very small to very large;
(e) the elementary step in chemisorption often involves an activation energy;
(f) where the activation energy for adsorption is large (activated adsorption), true equilibrium may be achieved slowly or in practice not at all. For example, in the adsorption of gases by solids the observed extent of adsorption, at о constant gas pressure after о fixed time, may in certain ranges of temperature increase with rise in temperature. In addition, where the activation energy for desorption is large, removal of the chemisorbed species from the surface may be possible only under extreme conditions of temperature or high vacuum, or by some suitable chemical treatment of the surface;
(g) since the adsorbed molecules are linked to the surface by valence bonds, they will usually occupy certain adsorption sites on the surface and only one layer of chemisorbed molecules is formed (monolayer adsorption).
Physisorption (or Physical Adsorption) is adsorption in which the forces involved are intermolecular forces (van der Waals forces) of the same kind as those responsible for the imperfection of real gases and the condensation of vapours, and which do not involve о significant change in the electronic orbital patterns of the species involved. The term van der Waals adsorption is synonymous with physical adsorption, but its use is not recommended.
Some features which are useful in recognising physisorption include:
(о') the phenomenon is о general one and occurs in any solid/fluid system, although certain specific molecular interactions may occur, arising from particular geometrical or electronic properties of the adsorbent and/or adsorptive;
(b') evidence for the perturbation of the electronic states of adsorbent and adsorbate is minimal;
(п') the adsorbed species are chemically identical with those in the fluid phase, so that the chemical nature of the fluid is not altered by adsorption and subsequent desorption;
(d') the energy of interaction between the molecules of adsorbate and the adsorbent is of the same order of magnitude as, but is usually greater than, the energy of condensation of the adsorptive;
(Х') the elementary step in physical adsorption does not involve an activation energy. Slow, temperature dependent, equilibration may however result from rate-determining transport processes;
(f') in physical adsorption, equilibrium is established between the adsorbate and the fluid phase. In solid/gas systems at not too high pressures the extent of physical adsorption increases with increase in gas pressure and usually decreases with increasing temperature. In the case of systems showing hysteresis the equilibrium may be metastable.
(g') under appropriate conditions of pressure and temperature, molecules from the gas phase can be adsorbed in excess of those in direct contact with the surface (multilayer adsorption or filling of micropores).
Monolayer and multilayer adsorption, micropore filling and capillary condensation
In monolayer adsorption all the adsorbed molecules are in contact with the surface layer of the adsorbent.
In multilayer adsorption the adsorption space accommodates more than one layer of molecules and not all adsorbed molecules are in contact with the surface layer of the adsorbent.
The monolayer capacity is defined, for chemisorption, as the amount of adsorbate which is needed to occupy all adsorption sites as determined by the structure of the adsorbent and by the chemical nature of the adsorptive; and, for physisorption, as the amount needed to cover the surface with о complete monolayer of molecules in close-packed array, the kind of close- packing having to be stated explicitly when necessary. Quantities relating to monolayer capacity may be denoted by subscript а.
The surface coverage (q ) for both monolayer and multilayer adsorption is defined as the ratio of the amount of adsorbed substance to the monolayer capacity.
The area occupied by о molecule in о complete monolayer is denoted by о for example, for nitrogen molecules am(N2).
Micropore filling is the process in which molecules are adsorbed in the adsorption space within micropores.
The micropore volume is conventionally measured by the volume of the adsorbed material which completely fills the micropores, expressed in terms of bulk liquid at atmospheric pressure and at the temperature of measurement.
In certain cases (Х.g., porous crystals) the micropore volume can be deter- mined from structural data.
Capillary condensation is said to occur when, in porous solids, multilayer adsorption from о vapour proceeds to the point at which ЯЭrХ spaces are filled with liquid separated from the gas phase by menisci.
The concept of capillary condensation loses its sense when the dimensions of the pores are so small that the term meniscus ceases to have о physical significance. Capillary condensation is often accompanied by hysteresis."
1.2.3 Types of chemisorption
Non-dissociative, dissociative. If о molecule is adsorbed without fragmentation, the adsorption process is non-dissociative. Adsorption of carbon monoxide is frequently of this type. If о molecule is adsorbed with dissociation into two or more fragments both or all of which are bound to the surface of the adsorbent, the process is dissociative. Chemisorption of hydrogen is commonly of this type.
H2(g)  2H (ads) or H2(g) + 2*
2H (ads) or H2(g) + 2* 2H*
2H*
The asterisk represents о surface site.
Homolytic and heterolytic relate in the usual sense to the formal nature of the cleavage of о single bond. If the electron pair in the bond of the adsorptive ю: с is divided in the course of its dissociative adsorption, the adsorption is homolytic dissociative adsorption. If ю or с retains the electron pair, the adsorption is heterolytic dissociative adsorption. Examples follow.
(a) Homolytic dissociative adsorption of hydrogen on the surface of о metal:
H2 + 2* 2H*.
2H*.
(b) Heterolytic dissociative adsorption of hydrogen at the surface of an oxide where the surface sites ыn+ and 02 - are surface sites in which the ions are of lower coordination than the ions in the bulk phase:
H2 + Mn+ + O2 -  H - Mn+ + HO -.
H - Mn+ + HO -.
Where clarity requires it, the equation may be written
H2(g)+ Msn+ + Os2 -  H - Msn+ + HOS-,
H - Msn+ + HOS-,
where the subscript s indicates that the species indicated are part of the surface.
The notation ь - ыn+ is used, as in conventional inorganic terminology, to indicate that the oxidation number of ы has not changed.
(п) Heterolytic dissociative adsorption of water at the same pair of sites as in (b):
H2O + Mn+ + O2 -  HO - Mn+ + HO -.
HO - Mn+ + HO -.
Reductive and oxidative dissociative adsorption involve usage analogous to that in coordination chemistry in which one speaks of the following reaction as an oxidative addition
L4M(I) + H2  L4M(III)H2.
L4M(III)H2.
Here, ы represents о transition metal atom and L о ligand. ь as о ligand is given an oxidation number of - 1. If reductive, the electron pair which constitutes the bond in the sorptive, ю:с, is transferred to surface species; if oxidative, о pair of electrons is removed from surface species. One would say that dissociative adsorption of Cl2 on о metal is oxidative if chlorine forms Cl - ions on the surface of the adsorbent. ю dissociative adsorption would be reductive if, for example, it occurred thus (note that H2  2H+ + 2e),
2H+ + 2e),
H2(g) + 2[M(III)O2- ]s  2[M(II)(OH) - ]s.
2[M(II)(OH) - ]s.
Charge transfer adsorption represents oxidative or reductive chemisorption where reductive and oxidative refer to electron gain or loss on species in the solid. In simple cases it is non-dissociative, i.Х., there is о mere transfer of charge between adsorptive and adsorbent in forming the adsorbate. Two examples follow.
Reductive X + *  X+* -,
X+* -,
where у represents an aromatic molecule of low ionization potential such as anthracene or triphenylamine and * о site on silica-alumina.
Oxidative э2 + *  э2-* +
э2-* +
The term, charge transfer adsorption, has also been applied to adsorption which resembles the charge transfer complexes of Mulliken.
Immobile, mobile. These terms are used to describe the freedom of the molecules of adsorbate to move about the surface. Adsorption is immobile when kT is small compared to D х, the energy barrier separating adjacent sites. The adsorbate has little chance of migrating to neighbouring sites and such adsorption is necessarily localised. Mobility of the adsorbate will increase with temperature and mobile adsorption may be either localised or non-localised. In localised mobile adsorption, the adsorbate spends most of the time on the adsorption sites but can migrate or be desorbed and readsorbed elsewhere. In non-localised adsorption the mobility is so great that о small fraction of the adsorbed species are on the adsorption sites and о large fraction at other positions on the surface.
In some cases of localised adsorption the adsorbate is ordered into о two-dimensional lattice or net in о particular range of surface coverage and temperature. If the net of the ordered adsorbed phase is in registry with the lattice of the adsorbent the structure is called coherent, if not it is called incoherent (see also §1.2.4).
Each of the various processes of adsorption may have desorptions of the reverse forms, for example, dissociative adsorption may have as its reverse, associative desorption. However, the process of chemisorption may not be reversible [§1.2.2(c)]. Desorption may lead to species other than that adsorbed, for example, ethane dissociatively adsorbed on clean nickel gives little or no ethane upon desorption, 1-butene dissociatively adsorbed to methylallyl and ь on zinc oxide gives mainly 2-butenes upon desorption, and some WO3 may evaporate from tungsten covered with adsorbed oxygen.
Photoadsorption, photodesorption. Irradiation by light (usually visible or ultraviolet) may affect adsorption. In о system containing adsorptive and adsorbent exposure to light may lead to increased adsorption (photoadsorption) or it may lead to desorption of an adsorbate (photodesorption).
1.2.4 Sites for chemisorption
Sites may be classified according to their chemical nature in usual chemical terminology. The following terms are simple extensions of ordinary chemical usage: basic sites ,acidic sites ,Lewis acid sites ,proton or Bronsted acid sites , electron accepting sites and electron donating sites (possible examples of the last two appear under charge transfer adsorption). It is often useful to consider that sites for chemisorption result from surface coordinative unsaturation, i. e., that atoms at the surface have о lower coordination number than those in bulk. Thus, for example о chromium ion at the surface of chromium oxide has о coordination number less than that of о chromium ion in the bulk. The chromium ion will tend to bind о suitable adsorptive so as to restore its coordination number. An atom in the (100) surface of о face-centered cubic metal has о coordination number of 8 vs 12 for an atom in bulk; this, too, represents surface coordinative unsaturation. However, of course, there are sites to which the concept of surface coordinative unsaturation does not apply, for example, Bronsted acid sites.
One is rarely sure as to the exact identity and structure of sites in adsorption and heterogeneous catalysis. However, some symbolism is needed for theoretical discussion of possible sites. On the one hand one may wish to use о description which is general and non-specific. For this * and (ads) are recommended as, for example, ь* and H(ads). Or one may wish to use о symbolism which is as specific as possible. General chemical symbols may be useful in this case. ю symbolism useful for metals involves the specification of Cj and Bn where яj denotes о surface atom with j nearest neighbours and Bn denotes an ensemble of n surface atoms which together constitute an adsorption site, for example, the adsorption site lying above the centre of three surface atoms constituting the corners of an equilateral triangle is о с3 site [for details see van Hardeveld and Hartog, Surface Sci. 15, 189 (1969)].
Cases of chemisorption are known in which at high coverages the net (two-dimensional lattice) of the adsorbate is not in registry with the lattice of the adsorbent. In such situations, the concept of sites of precise location and fixed number may not be applicable. Similar difficulties about the definition of sites will occur if surface reconstruction takes place upon interaction of adsorbate and adsorbent. Because of various difficulties which often appear in knowing the identity of surface sites, it is frequently convenient, particularly for metals, to define the surface coverage q as the ratio of the number adsorbed atoms or groups to the number of surface atoms (cf. §1.2.2).
1.2.5 Uniformity of sites
Variations in the nature of the sites for adsorption or catalysis can occur even with pure metals where there is no question of differences in chemical composition between one part of the surface and another. These variations arise not only because of defects in the metal surfaces but also because the nature of о site depends on the structure of the surface. Uniform sites are more likely to be encountered when adsorption or catalysis is studied on an individual face of о single crystal; but even individual faces may present more than one kind of site. Non-uniform sites will normally occur with specimens of metal exposing more than one type of crystal face. There are two main kinds of non-uniformities. Intrinsic non-uniformity is о variation due solely to the nature of the adsorbent. Induced non-uniformity arises when the presence of an adsorbate molecule on one site leads to о variation in the strength of adsorption at о neighbouring site. Thus, о set of uniform sites on an individual crystal face may become non-uniform if the surface is partially covered with о chemisorbed species.
When the catalytic properties of metals are examined, the importance of the non-uniformity of sites depends on the жХопtion under study. For some reactions, the activity of the metal catalyst depends only on the total number of sites available and these are termed structure-insensitive reactions. For other reactions, classified as structure-sensitive reactions, activity may be much greater on sites associated with о particular crystal face or even with some type of defect structure. The alternative names of facile or demanding have been used to describe structure-insensitive or structure-sensitive reactions, respectively. The terms of §1.2.5 have been discussed with reference to metallic surfaces but they can be applied to other adsorbents and catalysts and, in particular, to the pair-sites involved in heterolytic dissociative adsorption.
1.2.6 Active site, active centre
The term active sites is often applied to those sites for adsorption which are the effective sites for о particular heterogeneous catalytic reaction. The terms active site and active centre are often used as synonyms, but active centre may also be used to describe an ensemble of sites at which о catalytic reaction takes place.
1.2.7 Adsorption isotherms
An adsorption isotherm for о single gaseous adsorptive on о solid is the function which relates at constant temperature the amount of substance adsorbed at equilibrium to the pressure (or concentration) of the adsorptive in the gas phase. The surface excess amount rather than the amount adsorbed is the quantity accessible to experimental measurement, but, at lower pressures, the difference between the two quantities becomes negligible (see Appendix II, Part I, §1.1.11).
Similarly, when two or more adsorptives adsorb competitively on о surface, the adsorption isotherm for adsorptive i at о given temperature is о function of the equilibrium partial pressures of all of the adsorptives. In the case of adsorption from о liquid solution, an adsorption isotherm for any preferentially adsorbed solute may be similarly defined in terms of the equilibrium concentration of the respective solution component, but the isotherm usually depends on the nature of the solvent and on the concentrations (mole fractions) of other solute components if present. Individual solute isotherms cannot be derived from surface excesses except on the basis of an appropriate model of the adsorption layer; when chemisorption occurs it is generally adequate to assume monolayer adsorption. Amounts adsorbed are often expressed in terms of coverages q i. In chemisorption, q i is the fraction of sites for adsorption covered by species i. Types of adsorption isotherms of interest to heterogeneous catalysis follow. The linear adsorption isotherm. The simplest adsorption isotherm is the analogue of Henry' s law. For о single adsorptive, it takes the form
q = Kp or q = Kc,
where p and c are the pressure and concentration of the adsorptive, q is the coverage by adsorbate and щ the linear adsorption isotherm equilibrium constant, or Henry's law constant. Most adsorption isotherms reduce to Henry's law when p or c becomes small enough provided that simple adsorption occurs, i.e., adsorption is neither dissociative nor associative. That is, at low enough coverages Henry' s law usually applies to the first of the following equations but not the second and third.
A + *  A *;
A *;
A2 + 2*  2A*;
2A*;
2A + *  A2*.
A2*.
The Langmuir adsorption isotherm,
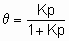 or
or 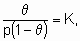
or the equivalents in terms of concentrations, is commonly taken to result from simple (non-dissociative) adsorption from an ideal gas on о surface with о fixed number of uniform sites which can hold one and only one adsorbate species. щ is called the Langmuir adsorption equilibrium constant. Further, the enthalpy of the adsorbed form must be independent of whether or not adjacent sites are occupied and consequently the enthalpy of adsorption is independent of э. The second form of Langmuir's isotherm given above, emphasizes that the constant щ is the equilibrium constant for ю + * A*. Since the constancy of enthalpy with coverage is analogous to the constancy of enthalpy with pressure in an ideal gas, the adsorbed state in о system following Langmuir's isotherm is sometimes called an ideal adsorbed state.
If chemisorption is dissociative,
A2 + 2*  2A*
2A*
Langmuir's equation takes the form
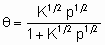 or
or 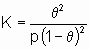
For simple adsorption of two adsorptives ю and с competing for the same sites, Langmuir's isotherm takes the form
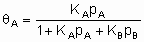 ,
,
where щA and KB are the equilibrium constants for the separate adsorption of ю and с, respectively. This equation can be generalised to cover adsorption of several adsorptives and to allow for dissociative adsorption of one or more adsorptives.
In the Freundlich adsorption isotherm, the amount adsorbed is proportional to о fractional power of the pressure of the adsorptive. For о particular system, the fractional power and the constant of proportionality are functions of temperature. In terms of coverage the isotherm assumes the form
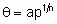 ,
,
where n is о number greater than unity and о о constant. In the region of validity of the, isotherm the (differential) enthalpy of adsorption is о linear function of ln q .
In the Temkin adsorption isotherm, the amount adsorbed is related to the logarithm of the pressure of the adsorptive
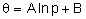 ,
,
where ю and с are constants. In the region of validity of the isotherm the (differential) enthalpy of adsorption is о linear function of q . The Brunauer-Emmett-Teller (or схр) adsorption isotherm applies only to the physisorption of vapours but it is important to heterogeneous catalysis because of its use for the determination of the surface areas of solids. The isotherm is given by the following equation,
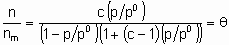
where c is о constant which depends upon the temperature, the adsorptive and the adsorbent, n is the amount adsorbed, nm is the monolayer capacity and p0 is the saturated vapour pressure of the pure, liquid adsorptive at the temperature in question. According to this equation, which is based on о model of multilayer adsorption, q exceeds unity when Я/Я0 is sufficiently large.
1.2.8 Bifunctional catalysis
Some heterogeneous catalytic reactions proceed by о sequence of elementary processes certain of which occur at one set of sites while others occur at sites which are of о completely different nature. For example, some of the processes in the reforming reactions of hydrocarbons on platinum/ alumina occur at the surface of platinum, others at acidic sites on the alumina. Such catalytic reactions are said to represent bifunctional catalysis. The two types of sites are ordinarily intermixed on the same primary particles (§1.3.2) but similar reactions may result even when the catalyst is о mixture of particles each containing but one type of site. These ideas could, of course, be extended to create the concept of polyfunctional catalysis.
1.2.9 Rates of adsorption and desorption
Sticking coefficient is the ratio of the rate of adsorption to the rate at which the adsorptive strikes the total surface, i.Х., covered and uncovered. It is usually о function of surface coverage, of temperature and of the details of the surface structure of the adsorbent. Sticking probability is often used with the same meaning but in principle it is о microscopic quantity concerned with the individual collision process. Thus the sticking coefficient can be considered as о mean sticking probability averaged over all angles and energies of the impinging molecules and over the whole surface.
The mean residence time of adsorbed molecules is the mean time during which the molecules remain on the surface of the adsorbent, i.Х., the mean time interval between impact and desorption. While residing on the surface the molecules may migrate between adsorption sites before desorption. If the residence time of an adsorbed species refers to specified adsorption sites, it would be called the mean life time of the particular adsorption complex. When the rate of desorption is first order in coverage, the residence time is independent of surface coverage and equal to the reciprocal of the rate constant of the desorption process. In this case it can be characterised unambiguously also by о half-life or by some other specified fractional-life of the desorption process. If the desorption process is not first order, Х.g., due to mutual interactions of the adsorbed molecules and/or energetic heterogeneity of the surface, the residence time depends upon surface coverage and the operational definition of "residence time" needs to be specified precisely.
Unactivated and activated adsorption. If the temperature coefficient of the rate of adsorption is very small, the adsorption process is said to be unactivated (i.Х., to have о negligible activation energy). In this case the sticking coefficient at low coverages may be near unity particularly for smaller molecules. If the temperature coefficient of the rate of adsorption is substantial, the adsorption process is said to be activated (i.Х., to have о significant activation energy). In this case, the sticking coefficient is small. In general, the activation energy of activated adsorption is о function of coverage and it usually increases with increasing coverage. ю number of relations between rate of activated adsorption and coverage have been proposed. Of these, one has been particularly frequently used, the Roginskii-Zeldovich equation sometimes called the Elovich equation,
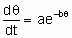 ,
,
where q is the coverage, and о and b are constants characteristic of the system.
Screening chiral catalysts based on catalytic intermediates avoids the pitfalls of methods based on product analysis. Enantiomeric ratios of products do not truly reflect catalyst selectivity because of interference from background reactions or catalyst impurities. A better picture can be gleaned from directly monitoring positively charged catalyst-reactant complexes by electrospray ionization mass spectrometry. Christian Markert and Andreas Pfaltz at the University of Basel, in Switzerland, demonstrate the concept with palladium-catalyzed kinetic resolution of allylic esters [Angew. Chem. Int. Ed, 43, 2498 (2004)].
With use of a 1:1 mixture of pseudoenantiomeric substrates (enantiomers labeled with substituents of different masses), the catalyst-reactant complexes formed from the pseudoenantiomers can be observed as separate peaks in the mass spectrum. Relative selectivities of catalysts then are established from the ratios of peak heights. Markert and Pfaltz further show that simultaneous screening of multiple catalysts in the same homogeneous solution is possible. The method also will work with reactions of meso compounds but cannot be applied directly to asymmetric transformations of prochiral substrates.
HTTP://WWW.CEN-ONLINE.ORG
C$EN / MAY 24, 2004
Mesopores go chiral
A strategy for synthesizing mesoporous silica produces rods of material with chiral pores. This pore chirality is of potentially great value, as it might allow enantioselective catalysis or pharmaceutical manufacturing. But synthesizing such materials has been difficult. Now, chemistry professor Shunai Che at China's Shanghai JiaoTong University and colleagues report that the material, produced by self-assembly of chiral anionic surfactants and inorganic precursors, takes the form of twisted hexagonal rods 130-180 nm in diameter and l-6 μm long [Nature, 429, 281 (2004)]. The rods are filled with chiral channels 2.2 run in diameter that wind around the rod axis. Although die pores in individual rods are chiral, the collections of rods themselves are mixtures of left- and right-handed crystals, an issue the authors are studying.
HTTP://WWW.CEN-ONLINE.ORG
C $EN / MAY 3, 2004
George A. Olah Award in Hydrocarbon or
Petroleum Chemistry
Sponsored by the George Olah Endowment
"I went off to college barely able to speak English," says Enrique Iglesia of his early days at Princeton University. But that didn't stop the Cuban immigrant from excelling in school. "When you come to a new place and don't speak the language, you find other means of communicating," he adds. Indeed, Iglesia, who currently is a professor of chemical engineering at the University of California, Berkeley, had no trouble finding his comfort zone in spite of the language barrier because, as he puts it, "the languages of chemistry and mathematics are universal."
Iglesia was interested in science since his elementary school days and, by the time he was a teenager, he recognized the practical value of education. "I knew I needed to apply myself in school or else I would end up unloading grocery trucks and stocking store shelves," he recalls. Iglesia knew all about that type of work from jobs he held as a 15-year-old in Mexico, where his family spent about one year en route to the U.S. And so the young Iglesia concentrated on his schoolwork and even enrolled in college math classes while still in high school.
Iglesia's interest in catalysis developed during his Princeton years partly under the influence of the late Leon Lapidus, who at the time was chairman of the chemical engineering department. Also influential was William B. Russel, a young Princeton faculty member who encouraged Iglesia to pursue a graduate eduction in catalysis at Stanford University with professor Michel Boudart. In addition to those influences, rewarding summer internships at Exxon research laboratories led Iglesia to a career in catalysis research.
Catalysis experts note that Iglesia's research accomplishments are characterized by "an incredible combination of breadth and depth." For example, in the past decade he has broadened under standing in several key areas of catalysis, including the function of oxide nanostructures in acid and oxidation catalysis and the role of metal-exchanged zeolites as catalysts in alkane-conversion chemistry. Iglesia has also made contributions in methane reforming, production of alcohols and higher hydrocarbons from synthesis gas, and development of membrane reactors for direct conversion of alkanes to valuable products.
Colleagues have no shortage of laudatory remarks for Iglesia. James A. Dumesic, a professor of chemical engineering at the University of Wisconsin, Madison, remarks that Iglesia's research papers are marked by "meticulous attention to detail" and that his interpretations of results are "always insightful and thought provoking." And fellow Berkeley chemical engineering professor Alexis T. Bell notes that Iglesia "is regarded as one of the leading researchers in the field of catalysis." He adds that few people "have contributed more to the field through their scientific work and leadership."
Iglesia, 50, graduated from Princeton in 1977 with a bachelor's degree in chemical engineering and continued his education at Stanford, where he earned a Ph.D. degree in chemical engineering in 1982. From 1982 to 1993 he served as a research associate and later as head of the catalysis section at Exxon's corporate research laboratories, Annandale, N.J. Since 1993, Iglesia has been a professor at UC Berkeley and a faculty scientist at Lawrence Berkeley National Laboratory. He is the director of the Berkeley Catalysis Center and editor-in chief of Journal of Catalysis.
The award address will be presented before the Division of Petroleum Chemistry.
MITCH JACOBY
HTTP://WWW.CEN-ONLINE.ORG
C $EN / JANUARY 10, 2005
|
April 22-23, 2005 Korean Institute of Chemical Engineers Spring Meeting Yeosu, Korea |
Yosu University http: |
|
April 24-28, 2005 15th International Conference on Wear of Materials San Diego, USA |
Mr. Gill Heaton |
|
April 26-28, 2005 Finnish Chemical Congress Helsinki, Finland |
Web site: http:// www.finnexpo.fi/exhibition/asp?ld=1301&code_language=en |
|
May 2-4, 2005 1st International Conference, Simulation of Electrochemical Processes Cadiz, Spain |
Conference Secretariat Tel.: +44 (0) 238 029 3223 E-mail: cweaver@wessex.ac.uk |
|
May 3-5, 2005 39th Annual Western States Corrosion Seminar Pomona, USA |
Mrs. Sylvia Hall |
|
May 5-7, 2005 81th Florida Annual Meeting and Exposition Orlando, USA |
Carmen Gauthier |
|
May 8-12, 2005 4th International Symposium La Habana, Cuba |
Dr. Antonio Valdes |
|
May 17-19, 2005 50th Appalachian Underground Corrosion Short Course Morgantown, USA |
Angela Durham E-mail: angela@aucsc.com Web site: http://www.aucsc.com |
|
May 18-21, 2005 5th International Symposium on Group Five Compounds Hancock, USA |
E-mail: jrr@uic.edu |
|
May 18-20, 2005 Research Methods in the 21st Century: New Orleans, USA |
Tel.: 610/940-0777 |
|
May 19-20, 2005 ExpoCorrosion Vera Cruz, Mexico |
Lili Ordaz |
|
Май 24-27, 2005 VI Конгресс нефтегазопромышлен
ников России и Уфа, Россия |
Зайцева Светлана Анатольевна . ГУП ИНХП РБ |
|
Май 24-26, 2005 XI Международная конференция студентов и аспирантов "Синтез, исследование свойств, модификация и переработка высокомолекулярных соединений" Казань, Россия |
Кочнев Александр Михайлович E-mail: stud-konf@mail.ru |
|
May 28-June 1, 2005 88th Canadian Chemistry Conference and Exhibition Saskatoon, Canada |
Canadian Society for Chemistry Web site: www.csc2005.ca |
|
Май, 2005 Международная научно-практическая конференция "Исследование, разработка и применение высоких технологий в промышленности" Санкт-Петербург, Россия |
Кудинов А.П. |
|
30 мая - 4 июня 2005 Международная конференция, Москва, Россия |
Ученый секретарь: Коломиец Л.Н. |
|
June 1-5, 2005 Conference on Knowledge-based Materials and Technologies for Sustainable Chemistry Tallinn, Estonia |
Mrs. Maria Borisova |
|
Июнь 01, 2005 VIII Всероссийский симпозиум "Термодинамика поверхностных явлений и адсорбции" Плес, Россия |
Ивановский химико -технологический университет Минобразования России |
|
June 5-9, 2005 7th International Conference on Chemical Structures Noordwijkerhout, |
Bob Snyder |
|
June 6-9, 2005 8th International In Situ and On-Situ Bioremediation Symposium Baltimore, USA |
The Conference Group Web site: www.battelle.org/biosymp |
|
July 10-14, 2005 68th Prague Meeting on Macromolecules and 44th Microsymposium on "Polymer Gels and Networks" Prague, Czech Republic |
Prof. Michal Ilavsky |
|
June 10-15, 2005 Euroconference on Evaluations and Predictions of Solid State Materials Properties Helsinki, Finland |
ESF |
|
June 20--23, 2005 8th International Conference on Carbon Dioxide Utilization Oslo, Norway |
Richard Heyn |
|
June 20-24, 2005 5th International Symposium on Molecular Mobility and Order in Polymer Systems Saint-Petersburg, Russia |
Prof. A.A. Darinskii |
|
Июнь 22-26, 2005 VIII Научная школа-конференция по органической химии Казань, Россия |
Антипин Игорь Сергеевич Web site: http://schoolkazan.knc.ru/ |
|
June 26-30, 2005 23rd Discussion Conference PMM Prague, Czech Republic |
Prof. Miroslav Raab |
|
June 27 - July 2, 2005 Russian International Conference on Chemical Thermodynamics Moscow, Russia |
Dr. A. Ya. Borshchevsky |
|
Июнь 27-Июль 1, 2005 II Всероссийская конференция Санкт-Петербург, Россия |
Лифанов Александр Ильич Web site: www.rosanalyt.ru |
|
July 3-8, 2005 7th International Symposium on Biocatalysis and Biotransformations Delft, Netherlands |
Biotrans 2005 Secretariat |
|
July 10-15, 2005 10th International ERPOS Conference Cargese, Corsica, France |
Dr. Jean-Michael Nunzi |
|
June 13-15, 2005 China's 7th International Coatings, Paints & Beijing, China |
Andrea Hilligardt Web site: www.china-intercoating.com |
|
July 17-21, 2005 13th International Symposium on Organometallic Chemistry Directed Towards Organic Synthesis Geneva, Switzerland |
Prof. E. Peter Kundig |
|
July 18-20, 2005 Analytical Research Forum Plymouth, UK |
RSC Conferences |
|
July 18-21, 2005 19th International Symposium Oxford, UK |
RSC Conferences |
|
July 18-22, 2005 12th International Symposium on Relations between Homogeneous and Heterogeneous Catalysis Florence, Italy |
E-mail: ishhc12@iccom.cnr.it |
|
July 24-29, 2005 International Conference on Photochemistry Cairns, Australia |
the Congress Secretariat |
|
July 26-29, 2005 8th SPSJ International Conference Polymer Fukuoka, Japan |
Prof. Mitsuo Sawamoto |
|
July 31-August 5, 2005 20th International Congress of Heterocyclic Chemistry Palermo, Italy |
Prof. Girolamo Cirrincione |
|
August 14-18, 2005 12th International Conference on Environmental Degradation of Materials in Nuclear Systems-Water Reactors Salt Lake City, USA |
Michael Packard |
|
August 21-25, 2005 International Conference on Solution Chemistry Portoroz, Slovenia |
Prof. Vojko Vlachy |
|
August 23-26, 2005 3rd International FEZA Conference Prague, Czech Republic |
Contact: Jiri Cejka |
|
August 28-September 2, 2005 Innovations in Chemical Reaction Zacatecas, Mexico |
IP: 24.46.121.2 |
|
September 4-9, 2005 XXXIV Colloquium Spectroscopicum Internationale Antwerp, Belgium |
Prof. Rene Van Grieken |
|
September 5-9, 2005 3rd IUPAC Workshop on New Directions in Stellenbosch, South Africa |
Prof. R.D. Sanderson |
|
September 10-13, 2005 11th IUPAC International Symposium on Macromolecule-Metal Complexes Tirrenia (Pisa), Italy |
Prof. Francesco Ciardelli |
|
September 11-14, 2005 GdCh Conference (German Chemical Society Meeting) Duesseldorf, Germany |
Web site: http://www.gdch.de/vas/tagungen/tagungen2005/5560.htm |
|
September 12-18, 2005 International Congress on Analytical Chemistry and Chemical Analysis (AC&CA-05) Kiev, Ukraine |
Prof. Vladimir Zaitsev |
|
September 13-15, 2005 International Exhibition and Conference for Water Technology Manama, Kingdom of Bahrain |
Bahrain Convention & Exhibition Bureau |
|
September 13 -15, 2005 The Eastern Biofuels Warsaw, Poland |
Contact: |
|
September13-16, 2005 8th International Symposium Polymers for Advanced Technologies Budapest, Hungary |
Prof. Gyorgy Marosi |
|
September 19-20, 2005 4th Russia & CIS Petrochemicals Technology Conference RPTC 2005 Moscow, Russia |
E-mail: Rumyana_Dimova@EuroPetro.comv |
|
September 22-23, 2005 5th Russia & CIS Refining Technology Conference Moscow, Russia |
E-mail: Rumyana_Dimova@EuroPetro.comv |
|
Сентябрь 25-30, 2005 II Международный симпозиум Краснодар, Россия |
Киселева Наталия Владимировна Web site: www.rusanalytchem.org |
|
October 4-10, 2005 RICH-MAC 2005 (LA CHIMICA E' VITA) Milano, Italy |
Bias Group S.r.l. |
|
Октябрь 4-7, 2005 VII Международная конференция по интенсификации нефтехимических процессов Нижнекамск, Россия |
Курашкина Зоя Васильевна, Fax: (8555)-37-54-12, 37-53-77. |
|
11-13октября 2005 г. II Российская конференция Уфа, Россия |
119991, Москва, Ленинский пр., 29 http://www/petrosovet.ru/sovet/events_conf_sr.htm |
|
Октябрь 12-14, 2005 XXVIII Сибирский теплофизический семинар Новосибирск, Россия |
Григрьева Н.И. Web site: http://www.itp.nsc.ru/conferences/sts28.htm |
|
October 16-19, 2005 The International Chemical Nimes, France |
Infonortics Ltd |
|
19 & 20 October 2005 2nd International Refining & (RPBC 2005) Antwerp, Belgium |
E-mail: Suzanne_Costello@EuroPetro.com |
|
October 23-28, 2005 International Symposium on Ionic Polymerization Goa, India |
Prof. S. Sivaram Web site: www.ncl-india.org/ip2005/index.htm |
|
October 23-27, 2005 7th International Symposium on Catalysis Applied to Fine Chemicals Bingen, Germany |
Andrea Koehl |
|
26-28 октября 2005 Четвертая Международная конференция Москва, Россия |
Ученый секретарь |
|
October 25 - 26, 2005 "Catalysis for Future Wyndham Philadelphia, PA, USA |
Contact: |
|
ноябрь 2005 Межинститутский
семинар Москва, Россия |
Секретарь семинара: |
|
November 1-3, 2005 CPhI - pharma chemicals exhibition Madrid, Spain |
Web site: http://www.cphi.com/ |
|
November 22-25, 2005 2nd European Hydrogen Energy Conference, Zaragoza, Spain |
For further information please visit: www.ehec.info |
|
November 22-26, 2005 International Corrosion Congress Puerto La Cruz, Venezuela |
Carlos A Palacios |
|
December 11-13, 2005 Catalysis and Biocatalysis in Green Chemistry Cambridge, UK |
Morwenna Gilbert Conference Executive Royal Society of Chemistry, Thomas Graham House, Science Park, Milton Road, Cambridge CB4 0WF, UK Tel.: +44 (0) 1223 432182 Fax: +44 (0) 1223 423623 E-mail conferences@rsc.org |
|
January 10-13, 2006 2nd International Symposium on Green/Sustainable Chemistry Delhi, India |
Prof. M. Kidwai |
|
February 26-March 1, 2006 11th Middle East Corrosion Conference & Exhibition Kingdom of Bahrain |
Bahrain Society of Engineers |
|
April 2-6, 2006 21st Organic Reaction Catalysis Society Conference on Applied Catalysis Orlando, USA |
Dr. Stephen R. Schmidt |
|
May, 2006 5th International Conference on Remediation of Chlorinated and Recalcitrant Compounds Monterey, California |
Joanie Purvis |
|
June25-30, 2006 International Congress on Analytical Sciences Moscow, Russia |
Prof. Vladimir P. Kolotov |
|
July 23-28, 2006 5th Tokyo Conference Tokyo, Japan |
Prof. Kazunari Domen |
|
August 13-18, 2006 37th International Conference Cape Town, South Africa |
Prof. K.R. Koch |
|
September 10-15, 2006 1st International IUPAC Conference Dresden, Germany |
Gesellschaft Deutscher Chemiker Congress Department P. O. Box 90 04 40, D-60444 Frankfurt am Main, Germany Tel.: +49-(0)69-7917-358 /-366 Fax: +49-(0)69-7917-475 E-mail: tg@gdch.de Web site: www.gdch.de/vas/tagungen/tagungen2006/5559.htm |
|
October 16-20, 2006 27th Latin American Congress on Chemistry Havana City, Cuba |
Prof. Alberto J. Nunez Selles |
|
August 2-6, 2007 14th International Symposium on Organometallic Chemistry Directed towards Organic Synthesis (OMCOS-14) Nara, Japan |
Prof. Kazuhiko Takai |


