
Терминология в гетерогенном катализе
под ред. Р.П.Бурвелла (продолжение)
Русский перевод
Ориганальная версия
О шестой рамочной программе Евросоюза
За рубежом
Приглашения на конференции
1.3 Composition, structure and texture of catalysts
1.3.1 General terms
Catalysts may be one-phase or multiphase. In the first case, they may be composed of one substance (for example, alumina or platinum black) or they may be а one-phase solution of two or more substances. In this case, the components of the solution should be given and joined by а hyphen (for example, silica-alumina).
Support. In multiphase catalysts, the active catalytic material is often present as the minor component dispersed upon а support sometimes called а carrier. The support may be catalytically inert but it may contribute to the overall catalytic activity. Certain bifunctional catalysts (§1.2.8) constitute an extreme example of this. In naming such а catalyst, the active component should be listed first, the support second and the two words or phrases should be separated by а solidus, for example, platinum/silica or platinum/silica-alumina. The solidus is sometimes replaced by the word "on," for example, platinum on alumina.
Promoter. In some cases, а relatively small quantity of one or more substances, the promoter or promoters, when added to а catalyst improves the activity, the selectivity, or the useful lifetime of the catalyst. In general, а promoter may either augment а desired reaction or suppress an undesired one. There is no formal system of nomenclature for designating promoted catalysts. One may, however, for example, employ the phase "iron promoted with alumina and potassium oxide."
А promoter which works by reducing the tendency for sintering and loss of area may be called а textural promoter (see §1.7.3).
Doping. In the case of semiconducting catalysts, а small amount foreign material dissolved in the original catalyst may modify the rate of а particular reaction. This phenomenon is sometimes called doping by analogy with the effect of similar materials upon semiconductivity.
1.3.2 Porosity and texture
Many but not all catalysts are porous materials in which most of the surface area is internal. It is sometimes convenient to speak of the structure and texture of such materials. The structure is defined by the distribution in space of the atoms or ions in the material part of the catalyst and, in particular, by the distribution at the surface. The texture is defined by the detailed geometry of the void space in the particles of catalyst. Porosity is а concept related to texture and refers to the pore space in а material. With zeolites, however, much of the porosity is determined by the crystal structure.
An exact description of the texture of а porous catalyst would require the specification of а very large number of parameters. The following averaged properties are often used.
With respect to porous solids, the surface associated with pores may be called the internal surface. Because the accessibility of pores may depend on the size of the fluid molecules, the extent of the accessible internal surface may depend on the size of the molecules comprising the fluid, and may be different for the various components of а fluid mixture (molecular sieve effect).
When а porous solid consists of discrete particles, it is convenient to describe the outer boundary of the particles as external surface.
It is expedient to classify pries according to their sizes
(iii) pores of intermediate size are called mesopores.
The terms intermediate or transitional pores, which have been used in the past, are not recommended.
In the case of micropores, the whole of their accessible volume may be regarded as adsorption space.
The above limits are to some extent arbitrary. In some circumstances it may prove convenient to choose somewhat different values.
Pore-size distribution is the distribution of pore volume with respect to pore size; alternatively, it may be defined by the related distribution of pore area with respect to pore size. It is an important factor for the kinetic behaviour of а porous catalyst and thus an essential property for its characterisation (see §1.6).
The computation of such а distribution involves arbitrary assumptions and а pore-size distribution should always be accompanied by an indication as to the method used in its determination. The methods usually involve either or both of the following: (i) adsorption - desorption isotherms of nitrogen or other adsorptives in conjunction with а particular model for conversion of the isotherm into а pore-size distribution, (ii) data obtained by the mercury porosimeter. The isotherm gives а pore-size distribution for mesopores. The mercury porosimeter gives а distribution covering macro- pores and larger mesopores. In both cases chat is measured is, strictly speaking, not the exact volume of pores having а given pore size, but the volume of pores accessible through pores of а given size. The relationship between these two functions depends on the geometrical nature of the pore system.
The specific pore volume is the total internal void volume per unit mass of adsorbent. Some of the pore volume may be completely enclosed, and thus inaccessible to molecules participating in а catalytic reaction.
The total accessible pore volume may be measured by the amount of adsorbate at the saturation pressure of the adsorptive, calculated as liquid volume, provided the adsorption on the external surface can be neglected or can be evaluated. The accessible pore volume may be different for molecules of different sizes. А method which is not subject to the effect of the external surface is the determination of the dead space by means of а non-sorbable gas (normally helium) in conjunction with the determination of the bulk volume of the adsorbent by means of а non-wetting liquid or by geometrical measurements.
Primary particles. Certain materials widely used as catalysts or supports consist of spheroids of about 10 nm (100 Å) in diameter loosely cemented into granules or pellets. The texture of these resembles that of а cemented, loose gravel bed. The 10 nm (100 Å) particles may be called primary particles.
Percentage exposed in metallic catalysts. The accessibility of the atoms of metal in metallic catalysts, supported or unsupported, depends upon the percentage of the total atoms of metal which are surface atoms. It is recommended that the term percentage exposed be employed for this quantity rather than the term dispersion which has been frequently employed.
Pretreatment and activation. Following the preparation of а catalyst or following its insertion into а catalytic reactor, а catalyst is often subjected to various treatments before the start of а catalytic run. The term pretreatment may, in general, be applied to this set of treatments. In some cases the word activation is used. It implies that the material is converted into а catalyst or into а very much more effective one by the pretreatment. Outgassing is а form of pretreatment in which а catalyst is heated in vacuo to remove adsorbed or dissolved gas. Calcination is а term which means heating in air or oxygen and is most likely to be applied to а step in the preparation of а catalyst.
1.4 Catalytic reactors
The vessel in which а catalytic reaction is carried out is called а reactor. Many different arrangements can be adopted for introducing the reactants and removing the products.
In а batch reactor the reactants and the catalyst are placed in the reactor which is then closed to transport of matter and the reaction is allowed to proceed for а given time whereupon the mixture of unreacted material together with the products is withdrawn. Provision for mixing may be required.
In a flow reactor, the reactants pass through the reactor while the catalysis is in progress. Many variations are possible.
The catalyst may be held in а packed bed and the reactants passed over the catalyst. А packed bed flow reactor is commonly called а fixed bed reactor and the term plug-flow is also used to indicate that no attempt is made to back-mix the reaction mixture as it passes through the catalyst bed. The main modes of operation of a flow reactor are differential involving а small amount of reaction so that the composition of the mixture is approximately constant throughout the catalyst bed, or integral involving а more substantial amount of reaction such that the composition of material in contact with the final section of the catalyst bed is different from that entering the bed.
In а pulse reactor, а carrier gas, which may be inert or possibly one of the reactants, flows over the catalyst and small amounts of the other reactant or reactants are injected into the carrier gas at intervals. А pulse reactor is useful for exploratory work but kinetic results apply to а transient rather than to the steady state conditions of the catalyst.
Several alternative modes of operation may be used to avoid the complications of the changing concentrations along the catalyst bed associated with integral flow reactors and each of these has а special name. In а stirred flow reactor, effective mixing is achieved within the reactor often by placing the catalyst in а rapidly-rotating basket. If the mixing achieved in this way is efficient, the composition of the mixture in the reactor will be close to that of the exit gases.
The same result can be reached by recirculation of the gas around а loop containing а fixed bed of catalyst, provided that the rate of recirculation is considerably larger then the rate of flow in and out of the loop. Under these circumstances, а substantial conversion to products can be obtained even though conditions in the bed correspond more closely to those associated with а differential rather than with an integral reactor. Another mode of operation involves a fluidised bed in which the flow of gases is sufficient to cause the bed of finely divided particles of catalyst to behave like а fluid. In а fluidised bed, the temperature is uniform throughout, although mixing of gas and solid is usually incomplete. It has special applications in cases where the catalyst has to be regenerated, е.g., by oxidation, after а short period of use. Continuous transfer of catalyst between two vessels (one used as reactor and the other for catalyst regeneration) is possible with а fluidised system. The stirred flow and the recirculation reactors are characterised ideally by very small concentration and temperature gradients within the catalyst region. The term, gradientless reactor, may be used to include both types.
All reactors, batch or flow, may be operated in three main ways in regard to temperature. These are isothermal, adiabatic and temperature-programmed. For the last, in а batch reactor the variation of temperature with time may be programmed, or in а fixed bed reactor the variation of temperature along the length of the bed may be controlled.
When reactors are operated isothermally the batch reactor is characterised by adsorbate concentrations and other aspects of the state of the surface which are constant in space (i.е., uniform within the catalyst mass) but which change with time. In the integral flow reactor with the catalyst at steady state activity, the surface conditions are constant with time but change along the bed. In the gradientless reactor at steady state, the surface conditions are constant in space and, if the catalyst is at а steady state, with time. In the pulse reactor, the catalyst is often not in а condition of steady state, concentrations change as the pulse moves through the bed, and there may be chromatographic separation of reactants and products.
In general, if heterogeneous catalytic reactions are to be conducted isothermally, the reactor design must provide for heat flow to or from the particles of catalyst so as to keep the thermal gradients small. Otherwise, temperatures within the catalyst bed will be non-uniform. The differential reactor and the various forms of the gradientless reactors are advantageous in this regard.
The types of reactors described above can, in principle, be extended to reactions in the liquid phase although the pulse reactor has been little used in such cases.
Reactions in which one reactant is gaseous, the other is in а liquid phase, and the catalyst is dispersed in the liquid phase, constitute а special but not unusual case, for example, the hydrogenation of а liquid alkene catalysed by platinum. А batch reactor is most commonly employed for laboratory scale studies of such reactions. Mass transport from the gaseous to the liquid phase may reduce the rate of such а catalytic reaction unless the contact between the gas and the liquid is excellent (see §1.6).
1.5 Kinetics of heterogeneous catalytic reactions
1.5.1 General terms
Consider а chemical reaction
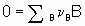 ,
,where n B is the stoichiometric coefficient (plus for products, minus for reactants) of any product or reactant В. The extent of reaction x is defined (see §11.1 of the Manual)
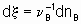 ,
,where nB is the amount of the substance В.
If rate of reaction is to have an unambiguous meaning, it should be defined as the rate of increase of the extent of reaction
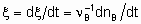
whereas the quantity dnB/dt may be called the rate of formation (or consumption) of B
То facilitate the comparison of the results of different investigators, the rates of heterogeneous catalytic reactions should be suitably expressed and the conditions under which they have been measured should be specified in sufficient detail. If the rate of the uncatalysed reaction is negligible, the rate of the catalysed reaction may be given as
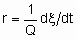 .
.If Q, the quantity of catalyst, is in mass,
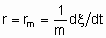
and rm is the specific rate of reaction which may be called the specific activity of the catalyst under the specified conditions. If Q is in volume,
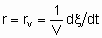 .
.The volume should be that of the catalyst granules excluding the intergranular space. If Q is in area,
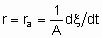 .
.where ra is the areal rate of reaction. If the total surface area of the catalyst is used, it should be preferably а ВЕТ nitrogen area. However, other types of specified areas may be employed, for ех. spic, the exposed metal area of а supported metallic catalyst. The exposed metal area is often estimated by selective chemisorption of а suitable sorptive, е.g., hydrogen or carbon monoxide.
The turnover frequency, N, (commonly called the turnover number) defined, as in enzyme catalysis, as molecules reacting per active site in unit time, can be а useful concept if employed with care. In view of the problems in measuring the number of active sites discussed in §1.2.4, it is important to specify exactly the means used to express Q in terms of active sites. А realistic measure of such sites may be the number of surface metal atoms on а supported catalyst but in other cases estimation on the basis of а ВЕТ surface area may be the only readily available method. Of course, turnover numbers (like rates) must be reported at specified conditions of temperature, initial concentration or initial partial pressures, and extent of reaction.
In comparing various catalysts for а given reaction or in comparing various reactions on а given catalyst, it may be inconvenient or impracticable to compare rates at а specified temperature since rates must be measured at temperatures at which they have convenient values. Therefore, it may be expedient to compare the temperatures at which the rates have а specified value.
In reactors in which the concentrations of reactants and products are uniform in space, the rate is the same on all parts of the catalyst surface at any specified time. In integral flow reactors, however, the rate on each element of the catalyst bed varies along the bed.
1.5.2 Selectivity
The term selectivity S is used to describe the relative rates of two or more competing reactions on а catalyst. Such competition includes cases of different reactants undergoing simultaneous reactions or of а single reactant taking part in two or more reactions. For the latter case, S may be defined in two ways. The first of these defines а fractional selectivity SF for each product by the equation
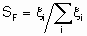 .
.The second defines relative selectivities, SR, for each pair of products by:
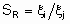 .
.In shape selectivity, which may be observed in catalysts with very small pores, the selectivity is largely determined by the bulk or size of one or more reactants. On zeolites, for example, the rate of reaction of alkanes with linear carbon chains may be much greater than that of those with branched chains.
1.5.3 Rate equations
Gaseous systems in which all concentrations are uniform in space and in which the reaction is irreversible will be considered first.
The rate x, besides being proportional to the quantity of catalyst, Q, is also in general а function of temperature Т and the concentrations сi or partial pressures рi of reactants, products and other substances if present:
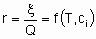 or
or
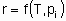
The statement of this equation is commonly called the rate equation or the rate law. Frequently, in heterogeneous catalysis, the function f is of the form
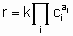 .
.where k is the rate constant which is а function of temperature but not of concentrations and аi (integral or fractional; positive, negative or zero) is the order of the reaction with respect to component i. This form of the rate law is called а power rate law. Often, however, а rate expression of different form is used. For example, or а reaction A + B ® products, the rate equation might be
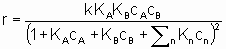 .
.This equation can be interpreted in terms Langmuir adsorption isotherms. It is assumed (see §1.5.4) that both reactants must be adsorbed in order to react and that KA and KB are the respective Langmuir adsorption equilibrium constants. The denominator allows for competition for sites between reactants and other substances (diluents, poisons and products) present in the system at concentrations cn with related adsorption equilibrium constants Кn. А rate law of this type is appropriately called a Langmuir rate law although it was made popular by Hinshelwood, Schwab, Hougen, Watson and others. Such rate laws are frequently used for systems in which the adsorptions may not obey the Langmuir adsorption isotherm. Under these circumstances, the rate laws can still provide а useful means of correlating experimental results but the values of the derived constants must be interpreted with caution.
For а single elementary process,
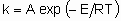 .
.where А is the frequency factor and Е the activation energy. Even though heterogeneous catalytic reactions rarely if ever proceed by а single elementary process, the same relation often applies to the overall rate constant. In such a case, however, А is not а frequency factor but should be called the preexponential factor and Е should be called the apparent activation energy.
Sometimes А and Е exhibit compensation, i.е., they change in the same direction with change in catalyst for а given reaction or with change in reaction for а given catalyst. А special case of compensation called the -rule occurs when, at least approximately,
 .
.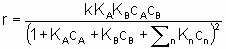 .
.This equation can be interpreted in terms Langmuir adsorption isotherms. It is assumed (see §1.5.4) that both reactants must be adsorbed in order to react and that KA and KB are the respective Langmuir adsorption equilibrium constants. The denominator allows for competition for sites between reactants and other substances (diluents, poisons and products) present in the system at concentrations cn with related adsorption equilibrium constants Кn. А rate law of this type is appropriately called a Langmuir rate law although it was made popular by Hinshelwood, Schwab, Hougen, Watson and others. Such rate laws are frequently used for systems in which the adsorptions may not obey the Langmuir adsorption isotherm. Under these circumstances, the rate laws can still provide а useful means of correlating experimental results but the values of the derived constants must be interpreted with caution.
For а single elementary process,
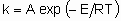 .
.where А is the frequency factor and Е the activation energy. Even though heterogeneous catalytic reactions rarely if ever proceed by а single elementary process, the same relation often applies to the overall rate constant. In such a case, however, А is not а frequency factor but should be called the preexponential factor and Е should be called the apparent activation energy. .
Sometimes А and Е exhibit compensation, i.е., they change in the same direction with change in catalyst for а given reaction or with change in reaction for а given catalyst. А special case of compensation called the q-rule occurs when, at least approximately,
 .
.where Т is the isokinetic temperature, the temperature at which all k's would be identical.
These considerations can be extended to reversible processes. They also apply to single phase, liquid systems, For the case, rather common in heterogeneous catalysts, in which one reactant is in а gas phase and the others and the products are in а liquid phase, application of the principles given above is straightforward provided that there is mass transfer equilibrium between gas phase and liquid phase, i.e., the fugacity of the reactant in the gas phase is identical with its fugacity in the liquid phase. In such case, а power rate law for an irreversible reaction of the form
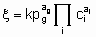 .
.may apply where the quantities have the same significance as before except that the gaseous reactant g is omitted from the ci's and entered as а pressure term with order аg.
The determination of rate of reaction in а flow system requires knowledge both of the feed rate, v, of а given reactant and of the fraction converted, x. The definition of feed rate as the amount of reactant fed per unit time to the inlet of the reactor is consistent with §;1.5.1. The rate of reaction is then given by
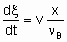 .
.where n Bis the stoichiometric coefficient of the reactant of which the fraction x is converted. Alternatively, one may proceed from rm, ri, and ra rather than dx /dt by defining the space velocities, vm, vv, and va where the vi's represent the rate of feed of the given reactant fed per unit mass, volume or surface area of the catalyst. The relation,
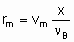 .
.gives the specific rate of reaction or, under specified conditions, the specific activity of the catalyst. Substitution of va or vv gives the areal rate of reaction or the rate divided by volume of the catalyst, respectively. Alternatively, space times, t m, t a, and t v, the reciprocals of the space velocities, may be used. "Contact time" and "residence time" are terms which may be misleading for flow systems in heterogeneous catalysis and should be avoided.
1.5.4 Kinetic aspects of mechanism
Of general convenience in the treatment of mechanisms are the notions of rate determining process or step and most abundant surface intermediate. The rate determining process is defined, as is usual in kinetics in general, as that single elementary process in the catalytic sequence which is not in equilibrium when the overall reaction is significantly displaced from equilibrium. If the surface of а catalyst has one set of catalytic sites, а particular intermediate is said to be the most abundant surface intermediate if the fractional coverage by that intermediate is much larger than coverages by the other intermediates. Of course, there is no guarantee that either а rate determining process or а most abundant surface intermediate will exist for any particular reaction under а particular set of conditions.
The term reaction centre may be used to include both vacant and occupied catalytic sites. The sum of the surface concentrations of reaction centres on the surface of а catalyst is а constant L. Thus, if species m at а surface concentration Lm is the most abundant surface intermediate,
Lm + Lv »
L, where Lv is the surface concentration of vacant reaction centres.
Langmuir-Hinshelwood mechanism. This represents a somewhat anomalous use of the term mechanism to specify relative magnitudes of rate constants. In a Langmuir-Hinshelwood mechanism, all adsorption-desorption steps are essentially at equilibrium and a surface step is rate determining. Such a surface step may involve the unimolecular reaction of a single adsorbate molecule or the reaction of two or more molecules on adjacent sites with each other. Where the adsorption processes follow Langmuir adsorption iso therms, the overall reaction will follow some kind of a Langmuir rate law (§1.5.3). However, the term Langmuir-Hinshelwood mechanism may cover situations in which Langmuir adsorption isotherms do not apply.
1.5.5 Non-uniformity of catalytic sites
A characteristic of a catalytic surface is that its sites may differ in their thermodynamic and kinetic properties. In the kinetic description of catalytic reactions on non-uniform surfaces, a parameter a is frequently used to connect changes in the activation energy of activated adsorption with the enthalpy of the adsorption
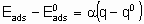 .
.where 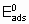 is the energy of activation and -q0 is the enthalpy of adsorption on the uncovered surface. Eads and q apply to the surface with the same value of a
. In practice the equation may apply only over a restricted range of q
. Sometimes a
is defined as in the equation above but in terms of Gibbs energies of activation and adsorption, respectively. The name transfer coefficient has been used by electrochemists to represent a
in another related situation.
is the energy of activation and -q0 is the enthalpy of adsorption on the uncovered surface. Eads and q apply to the surface with the same value of a
. In practice the equation may apply only over a restricted range of q
. Sometimes a
is defined as in the equation above but in terms of Gibbs energies of activation and adsorption, respectively. The name transfer coefficient has been used by electrochemists to represent a
in another related situation.